Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 8
A conexão AC tem seção transversal retangular uniforme 1/8 in de espessura e 1 in de altura. Determine a tensão normal na porção central da conexão.
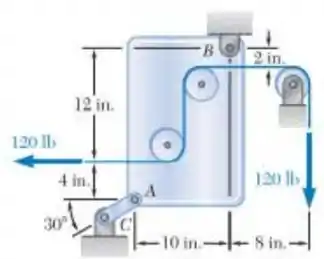
Passo 1
E ai gurizada tudo belezinha??? O exercício para encontrarmos a tensão pedida pelo exercício temos que antes de mais nada calcular o mento em B para encontrarmos a força da conexão AC, então partiu!!!
Passo 2
Gurizada agora para encontrarmos a tensão vamos relembrar a equação:
Mas notem que ainda não calculamos a área então antes de determinar a tensão partiu calcular a área...
como são duas partes paralelas multiplicaremos por 2 e teremos
Agora sim podemos calcular:
Resposta
Exercícios de Livros Relacionados
Para a barra composta do Problema 2.107, se P é aumentada gradualmente desde zero até que o deslocamento do ponto C atinja um valor máximo de δ m = 0,3m m e depois diminuída novamente até zero, determ
Duas barras de aço temperado, cada uma com espessura de 5 mm, são coladas a uma barra de aço doce de 12 mm. Essa barra composta é submetida a uma força axial centrada de intensidade P, conforme mostra
A barra AB consiste em duas partes cilíndricas AC e BC, cada uma cm seção transversal de área igual a 1,750m m ² ². A parte AC é feita de um aço doce com E = 200G P ae σ E = 250M P a , e parte CB é fe
Resolva o Problema 2.113 sabendo que a = 1,76m e que a intensidade da força Q aplicada em B é aumentada gradualmente de zero até 135k N .
A barra rígida ABC é suportada por duas barras elástica, AD e BE, de seção transversal retangular uniforme de 37,5x6m m e feitas de uma aço doce considerado elastoplástico, com E = 200G P aeσ E = 250M