Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 16

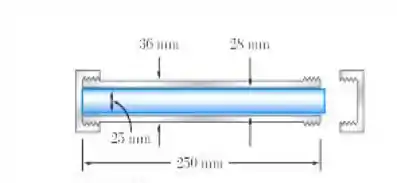
Um tubo de alumínio com 250 mm de comprimento (   E = 70   G P a ) , 36 mm de diâmetro externo de 28 mm de diâmetro interno pode ser fechado em ambas as extremidades por meio de tampas com rosca simples de 1,5 mm de passo. Com uma das tampas aparafusada e apertada, uma barra sólida de latão (   E = 105   G P a ) de 25 mm de diâmetro é colocada dentro do tubo e uma segunda tampa é aparafusada. Como a barra é ligeiramente mais longa que o tubo, observa-se que a tampa precisa ser forçada contra a barra girando-a 1 4 de volta para que o tubo fique bem fechado. Determine (a) a tensão normal média no tubo e na barra e (b) as deformações do tubo e da barra.

Passo 1

Fala aí galerinha tudo beleza? Para determinarmos a tensão , primeiramente temos que calcular a área do tubo e da tampa

A t u b o = π 4   x   d o 2 - d i 2 = π 4   x   36 2 - 28 2 = 402,12 m m 2 = 402,12   x   10 - 6 m 2

A t a m p a = π 4   x   d 2 = π x 4   x   ( 25 ) 2 = 490,87 m m 2 = 490,87   x   10 - 6 m 2

Calculando o alongamento de ambas as partes temos:

δ t u b o = P L E t u b o A t u b o = P 0,250 70   x   10 9 x 402,12   x   10 - 6 = 8,8815   x   10 - 9 P

δ t a m p a = P L E A = P 0,250 105   x   10 6 x 490,87   x   10 - 6 = - 4,8505   x   10 - 9 P

δ * = 1 4 x   1,5   m m = 0,375 m m = 375   x   10 - 6 m (1) δ t u b o =   δ * +   δ t a m p a       (2)

Para encontrarmos P temos que substituir 1 em 2, temos:

8,8815   x   10 - 9 P + 4,8505   x   10 - 9 P = 375   x   10 - 6 P =   0,375   x   10 - 3 8,8815 + 4,8505   x   ( 10 - 9 ) = 27,308   x   10 3 N

Passo 2

Agora sim gurizada como encontramos a força P no passo 1 podemos encontrar a tensão dos componentes e as suas respectivas deformações.

  1. σ t u b o =   P A = 27,308   x   10 3 402,12   x   10 - 6 = 67,9   x   10 6 P a
  2. σ t a m p a =   P A =   - 27,308   x   10 3 490,87   x   10 - 6 = - 55,6   x   10 - 6 m

  3. δ t u b o = 8,8815   x   10 - 9   x   27,308   x   10 3 = 242,5   x   10 - 6 m

δ t a m p a =   - 4,8505   x   10 - 9   x   27,308   x   10 3 =   - 132,5   x   10 - 6 m

Resposta

  1. σ t u b o = 67,9   M P a σ t a m p a =   - 55,6   M P a

  2. δ t u b o = 0,243   m m δ t a m p a =   - 0,1325   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O estado plano de tensões indicado é esperado em um componente de ferro fundido. Sabendo-se que para a classe de ferro fundido usada σ u t = 170MPae σ u c = 340MPa, e usando o critério de Mohr, determ
O estado plano de tensões indicado é esperado em um componente de ferro fundido. Sabendo-se que para a classe de ferro fundido usada σ u t = 80MPae σ u c = 200MPa, e usando o critério de Mohr, determi
O estado plano de tensões indicado é esperado em um componente de ferro fundido. Sabendo-se que para a classe de ferro fundido usada σ u t = 170MPae σ u c = 340MPa, e usando o critério de mohr, determ
O estado plano de tensões indicado é esperado em um componente de ferro fundido. Sabendo-se que para a classe de ferro fundido usada σ u t = 80MPae σ u c = 200MPa, e usando o critério de Mohr, determi
Uma barra de alumínio fundido é feita de uma liga em que σ u t = 70MPa e σ u c =140MPa e é sujeito a um torque T e a uma força axial P de 50kN. Usando o critério de Mohr, determinar a intensidade do t