Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 14
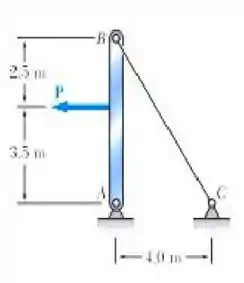
O cabo BC de 4 mm de diâmetro é feito de um aço com . Sabendo que a máxima tensão no cabo não pode exceder 190 MPa e que a deformação do cabo não deve exceder 6 mm, determine a máxima força P que pode ser aplicada conforme mostra a figura.
Passo 1
Fala aí gurizada tudo belezinha? Vem comigo encontrarmos primeiramente o comprimento do cabo BC, let’s go!!!
Agora vamos desenhar o diagrama de corpo livre para podermos calcular o somatório do momento em A.
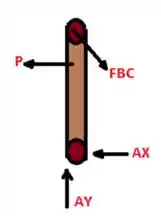
Considerando a tensão, , vamos determinar a área:
Agora podemos determinar a força no trecho BC
Passo 2
Considerando o alongamento
Isolando temos:
Menor valor de governa.
Resposta
Exercícios de Livros Relacionados
Um reservatório esférico de gás, feito de aço, tem um diâmetro externo de 5m e uma espessura da parede 10mm. Sabendo-se que a pressão interna é de 400kPa, determinar a máxima tensão normal e a máxima
Resolver o Prob. 6.86, usando o critério da máxima tensão de cisalhamento.
Resolver o Prob. 6.94, considerando que o sentido da força P é o inverso.
O estado de tensões mostrado irá ocorrer em um componente de alumínio fundido. Sabendo-se que para a liga de alumínio usada σ u t = 60MPae σ u c = 120MPa, e usando o critério de Mohr, determinar a ten
O estado de tensões mostrado irá ocorrer em um componente de alumínio fundido. Sabendo-se que para a liga de alumínio usada σ u t = 60MPae σ u c = 120MPa, e usando o critério de Mohr, determinar a ten