Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 111

Um tubo de alumínio com diâmetro externo de 3 in. suportará uma ação de 10 kips com uma excentricidade e = 0,6   i n . Sabendo que o estoque de tubos disponíveis para uso é composto por elementos da liga 2014-T6 e tem espessuras de parede em incremento de 1 16 i n . Até 1 2 i n . , determine o tubo mais leve que pode ser utilizado. Utilize o método das tensões admissíveis.

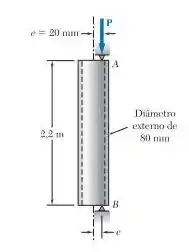
Passo 1

O enunciado pede que a gente determine o tubo mais leve que pode ser utilizado, temos então os seguintes dados:

L e = 6   f t = 72   i n .                   c o = 1 d d o = 1,500 i n . = c

c i = c o - t = 1,500 - t

A = π ( c o 2 - c i 2                     I = π 4 ( c o 2 - c i 2 )

Passo 2

Temos então os dados abaixo :D

t = 1 4 i n . = 0,25 i n .                                                                         c i = 1,250 i n .

A = 2,1598 i n 2             I = 2,0586 i n 4

r = I A = 0,97629   i n .

L r = 72 0,97629 = 72,748 > 55                

σ a l l = 55,400 L r 2 = 55,400 73,748 2 = 10,186 k s i

Passo 3

Continuando :D

P a l l A + M c I = P a l l A + P a l l e c I = 1 2,1598 + 0,6 1,500 2,0586 P a l l = 0,9002 P a l l

P a l l = σ a l l 0,9002 = 10,186 0,9002 = 11,315 k p s > 10 k i p s

Já que P a l l é quase proporcional a espessura t ,

t 0,25 ≈ 10 11,315                 t ≈ 0,221   i n .   > 3 16   i n .   = 0,1875   i n .

3 16 i n .     e s p e s s u r a   s e r i a   m u i t o   p e q u e n a .   U s e   t = 1 4 i n .

Resposta

1 4 i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um membro em compressão tem a seção transversal mostrada e um comprimento efetivo de 2m. Sabendo-se que a liga de alumínio usada é 2014-T6, determinar a carga centrada admissível.
Um membro em compressão de comprimento efetivo igual a 9 m é obtido soldando-se duas placas de aço de 10 mm de espessura a um perfil laminado de aço w250 x 80, como mostrado. Sabendo que σ= 320 MPa e
Resolver o problema 11.100 assumindo que o comprimento efetivo do membro comprimido é aumentado para 2,75 m.
Um membro em compressão de comprimento efetivo igual a 9 m é obtido soldando-se duas placas de aço de 10 mm de espessura a um perfil laminado de aço w250 x 80, como mostrado. Sabendo que σ= 320 MPa e
Um membro em compressão tem a seção transversal mostrada em um comprimento efetivo de 1,5m. Sabendo-se que a liga de alumínio usada é 6061 - t 6 , determinar a carga a carga centrada admissível.