Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 124

O tubo de 2   m de comprimento é feito de um material elástico-plástico como mostra a figura. Determine o torque aplicado T que submete o material da borda externa do tubo a uma deformação por cisalhamento de γ m a x = 0,008   r a d . Qual seria o ângulo de torção permanente do tubo quando o torque for removido? Faça um rascunho da distribuição da tensão residual no tubo

Passo 1

Dados da questão: Material elástico-plástico. L = 2   m ,   r O = 45   m m ,   r i = 40   m m ,   τ e = 240   M P a ,   γ e = 0,003   r a d ,   γ m a x = 0,008   r a d .

A questão pede:

  • Torque plástico
  • O ângulo de torção residual
  • Um esquema das tensões

A estratégia de resolução será: Primeiro identificar o torque plástico, e com isso determinar o ângulo de torção elástico. Depois utilizar a equação 5.15 para determinar a recuperação elástica do tubo.

E no último passo, fazemos a distribuição de tensão no tubo.

Passo 2

O torque plástico que atua sobre eixo pode ser calculado pela equação 5.23

T P = 2 π ∫ r i r O τ ⋅ ρ 2 d ρ

Como não há núcleo elástico, a tensão é constante e igual à tensão de escoamento: τ = τ e

T P = 2 π ∫ r i r O τ e ⋅ ρ 2 d ρ

T P = 2 π τ e ∫ r i r O ρ 2 d ρ

T P = 2 π τ e ⋅ ρ 3 3 r i r O    

T P = 2 3 π τ e ⋅ ( r O 3 - r i 3 )  

T P = 2 3 π ⋅ 240 ⋅ 10 6 ⋅ 0,045 3 - 0,040 3 ⋅ P a ⋅ m 3    

T P = 13634,52   N m

Passo 3

Já que a parte externa sofre a deformação máxima, podemos encontrar o ângulo de torção plástica do eixo:

ϕ p = γ m a x L r o

ϕ p = 0,008 2 0,045 ⋅ r a d ⋅ m m

ϕ P = 0,3556   r a d

Passo 4

Vamos calcular o momento de inércia:

J = π 2 r O 3 - r i 3

J = π 2 0,045 3 - 0,040 3

J = 2,42 ⋅ 10 - 6   m 4

Passo 5

Olhe pro gráfico fornecido na questão:

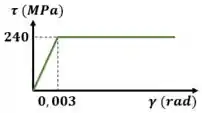
Pela zona linear do gráfico podemos calcular o módulo de cisalhamento usando a lei de hooke

G = τ e γ e

G = 240   M P a 0,003

G = 80   G P a

Passo 6

Quando o torque for removido, o tubo vai se “des-deformar”! Essa recuperação de deformação tem comportamento elástico e funciona como se um torque de intensidade T P fosse aplicado no sentido inverso.

Podemos aplicar a equação 5.15 para encontrar o valor da deformação recuperada

ϕ ' = T L G J

ϕ ' = 13634,5 ⋅ 2 80 ⋅ 10 9 ⋅ 2,42 ⋅ 10 - 6 ⋅ N m ⋅ m P a ⋅ m 4

ϕ ' = 0,1409   r a d

Passo 7

A deformação residual é a diferença entre a deformação plástica e a recuperação elástica

ϕ r = ϕ p - ϕ '

ϕ r = 0,3556 - 0,1409

ϕ r = 0,2147   r a d

ϕ r = 12,3 º

Passo 8

O esquema consiste em analisar o eixo em três momentos: Durante o esforço plástico (a), durante a recuperação (b) e o instante final (c)

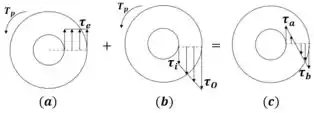
Tensão no regime plástico

τ = τ e = 240   M P a

Tensão no regime elástico

τ i = T P ⋅ r i J = 13634,5 ⋅ 0,040 2,42 ⋅ 10 - 6 ⋅ N m ⋅ m m 4 ⇒ τ i = 225,36   M P a

τ o = T P ⋅ r o J = 13634,5 ⋅ 0,045 2,42 ⋅ 10 - 6 ⋅ N m ⋅ m m 4 ⇒ τ o = 253,53   M P a

Tensão residual

τ a = τ e - τ i = 240 - 225,36 ⇒ τ a = 14,64   M P a

τ b = τ O - τ e = 253,35 - 240 ⇒ τ b = 13,35   M P a

Resposta

ϕ r = 12,3 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque de pressão feito de aço mostrado na figura tem um diâmetro interno de 750m m e uma espessura de parede de 9m m . Sabendo que as emendas de solda de topo formam um ângulo β = 50 ° com eixo lon
Resolva o problema 7.120 considerando que a intensidade P das duas forças é elevada para 133,4k N .
No problema 7,124 , determine a máxima tensão nromal e a máxima tensão cisalhante no ponto L .
O tanque de ar comprimido A B tem um diâmetro externo de 250m m e espessura de parede de 8m m . Ele é equipado com um anel no qual é aplicada uma força P de 40k N horizontal em B . Sabendo que a press
Um anel de latão com diâmetro externo de 127m m e espessura de 6,35m m se encaixa exatamente dentro de um anel de aço com diâmetro interno de 127m m e 318m m de espessura, quando a temperatura de ambo