Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 40
Para o tubo do Prob.1.39, sabendo-se que as máximas tensões nas direções normal e tangencial, no cordão de solda são e , respectivamente, determine a intensidade da maior força axial P que pode ser aplicada ao tubo.
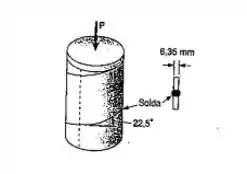
Passo 1
Vamos fazer um desenho e dar uma olhada em como se distribuem as forças no plano que nos interessa.
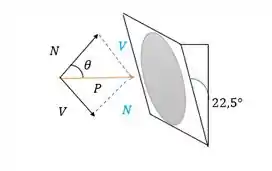
Onde , e pela geometria do problema a gente consegue observar que ele esta entre P e N.
Quando temos o ângulo dessa forma, a decomposição das forças se dá:
Passo 2
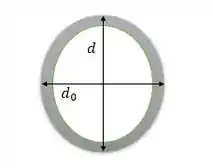
A área sofrera distorção, e é parecido com o que acontece com uma seção retangular. Somente a vertical distorce, assim:
Onde é o diâmetro distorcido e é o diâmetro inicial.
O plano oblíquo será então uma elipse, pois na horizontal o diâmetro não se distorce.
Precisaremos das medidas internas por se tratar de um tubo:
Enfim as áreas:
E a área final será:
Passo 3
Agora que temos a área que nos interessa vamos calcular o peso para cada tensão admissível:
E para a tensão cisalhante:
Pegamos o menor entre eles, que é: