Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas de Revisão - Ex. 60

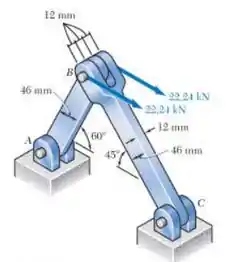
Duas forcas horizontais de 22,24 kN são aplicadas ao pino B do conjunto mostrado na figura. Sabendo que é utilizado um pino de 20,32 mm de diâmetro em cada conexão, determine o valor Maximo da tensão normal media (a) a haste AB e (b) na haste BC.

Passo 1

Fala ai gurizada primeiramente vamos desenhar o diagrama de corpo livre...

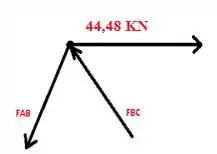
Aplicando a lei dos senos:

F A B s e n 45 ° = F B C s e n 60 ° = 44,48 s e n 75 °

F A B =   32,56   k N

F B C = 39,88   k N

Passo 2

Calculando a tensão na barra AB:

      A =   46   –   20,32 × 12 = 308 m m 2 = 308 × 10 - 6 m ²

Tensão em AB:

  1. σ A B = F A B A =     32,56 × 10 3 308 × 10 - 6 = 1,0 × 10 8   P a = 100 × 10 6 P a

σ A B = 100   M P a

Em BC temos:

Área de seção transversal é: (repara que são duas partes, então multiplica por 2)

  A = 2 × 46 - 20,32 × 12 = 616   m m 2 = 616 × 10 - 6   m ²

(b )

  σ B C = - F B C A =   - 39 ,   88 × 10 3 616 × 10 - 6 = - 6,47   × 10 7   P a = - 64,7 × 10 6 P a

  σ B C = - 64,7   M P a

Resposta

  1. σ A B = 100   M P a
  2. σ B C = - 64,7   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a amostra do Prob 2.14, determinar a maior carga P admissível, se a deformação na porção AB e a deformação total da amostra não devem exceder a 0,2 m m e 1m m , respectivamente.
Cada uma das quatro hastes de ligação verticais, conectadas às duas vigas horizontais, são de alumínios ( E = 70 G P a ) e têm uma seção transversal retangular de 10 × 40 m m . Para o carregamento mos
Para a treliça de aço E = 200 G P a e carregamento mostrado, determinar as deformações nos membros B D e D E , sabendo-se que suas seções transversais tem 1300 m m 2 e 1950 m m 2
Um tubo cilíndrico de poliestireno de parede fina E = 3,1G P a , com 3,2m m de espessura e uma placa rígida circular (é ostrada apenas parte dela), são usadas para suportar uma barra de aço A B ( E =
Um tubo cilíndrico de poliestireno de parede fina E = 3,1G P a , com 3,2m m de espessura e uma placa rígida circular (é ostrada apenas parte dela), são usadas para suportar uma barra de aço A B ( E =