Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas de Revisão - Ex. 63
O conjugado M de intensidade 1500 N m é aplicado à manivela de um motor. Para a posição mostrada, determine (a) a força P necessária para manter o sistema do motor em equilíbrio e (b) a tensão normal media na biela BC, que tem uma seção transversal uniforme de 450 mm².
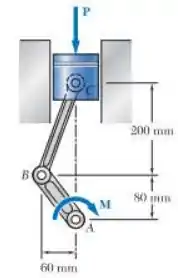
Passo 1
Falai gurizada tudo bem? Primeiramente vamos desenhar o diagrama de corpo livre
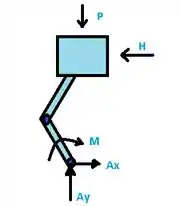
Agora partiu calcular o momento em A, para encontrarmos H.
Passo 2
Gurizada agora para facilitar os cálcilos e encontrarmos a força em BC vamos esboçar um triangulo, com suas respectivas forças, vejam:
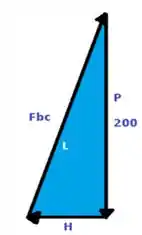
Por pitagoras temos que:
Então temos:
Passo 3
Para encontrarmos a tensão compressive, temos que:
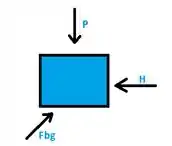
Agora partiu calcular a tensão:
Resposta
- P = 17,86 kN
- = -41,4MPa
Exercícios de Livros Relacionados
Para a montagem e carregamento do problema 1.13, determine (a) a tensão de cisalhamento média no pino B; (b) a tensão de esmagamento em B, na barra de ligação BE; (c) A tensão de esmagamento em B, na
O cilindro hidráulico CF, que controla parcialmente a posição da barra cilíndrica DE, está completamente distendido na posição mostrada. A barra BD tem 15mm de espessura e está ligada em C, por um par
Os membros AB e BE de treliça mostrada são de barras de aço ( E = 200 G P a ) com 25m m de diâmetro. Para o carregamento mostrado, determinar o alongamento de ( a ) barra AB; ( b ) barra BE
Um cabo homogêneo de comprimento L e seção transversal uniforme é preso por uma de suas extremidades. (a) Expressando por ρ a densidade (massa por volume) do cabo e por E o módulo de elasticidade, det
Um cabo homogêneo de comprimento L e seção transversal uniforme é preso por uma de suas extremidades. (a) Expressando por ρ a densidade (massa por volume) do cabo e por E o módulo de elasticidade, det