Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 125
Uma única força vertical P é aplicada a um poste curto de aço conforme mostrado. Extensômetro localizados em A, B e C indicam as seguintes deformações:
Sabendo que , determine:
- A intensidade de P;
- A linha de ação de P
- A deformação correspondente a aresta escondida do poste, onde .
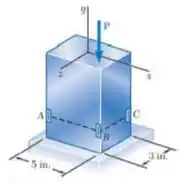
Passo 1
Para essa questão temos três itens a serem resolvidos, primeiro determinar a força que causa essas deformações nos pontos A, B e C e o respectivo braço de alavanca que causaria essas deformações.
Para isso temos que saber o seguinte, se temos deformações, temos como calcular tensões pela seguinte fórmula:
Mas pensa no seguinte, se queremos determinar as cargas que agem na seção, e temos as tensões, podemos pensar da seguinte forma.
- As tensões vão ser causadas pela carga axial que age na nossa seção, ou seja, a carga P espalhada pela área da seção,
- E como essa carga P tem dois braços de alavanca, ela também vai causar dois momento fletor, que também vai contribuir na nossa tensão.
Sendo assim, também podemos escrever as nossas tensões pela seguinte equação.
Tendo essas três relações, precisamos agora começar a determinar o que temos, sendo assim podemos anotar no próximo passo.
Passo 2
- Dados do enunciado
- Dados da seção
- Dados de z e x para determinar o cálculo das tensões em A, B e C.
Pelos dados do enunciado temos que:
Sabemos que a nossa seção é dada com as seguintes dimensões.
A área da seção vai ser feita da seguinte maneira:
E o momento de inércia é calculado pela seguinte equação:
Sendo assim teremos que:
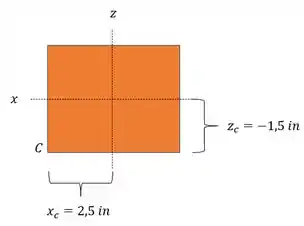
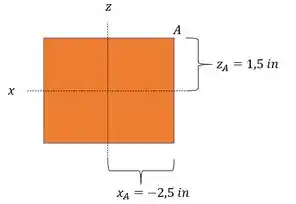
Calculando as tensões pela deformação, teremos que:
Analisando o outro grupo de fórmulas, temos que:
Substituindo temos que:
E assim tem-se que:
Resolvendo o sistema, obtemos que:
E assim resolvemos o item a) descobrimos o valor da carga P.
Passo 3
Para o item B) precisamos da linha de ação, e como temos o momento fletor, podemos lembrar que o cálculo de momento para cada uma das direções pode ser dado por:
Assim substituindo o que temos, teremos que as linhas de ações serão dadas por:
E assim resolvemos o item B)
Passo 4
E para o item C), queremos determinar a deformação no ponto escondido, para isso temos que lembrar que a equação de tensão é determinada por:
Pelo enunciado nos é dito que e o resto dos valores nos já temos, assim substituindo teremos que:
E sabemos que:
Substituindo: