Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 137
O momento é aplicado a uma viga de seção transversal mostrada, em um plano formado um ângulo com a vertical. Determinar:
- A tensão no ponto A;
- A tensão no ponto B;
- O ângulo que a linha neutra forma com o plano horizontal.
Passo 1
Para determinação de tensões em elementos que estão sujeitos a momentos fletores inclinados, ou ainda, momentos fletores oblíquos, ou momentos fletores assimétricos, temos a seguinte fórmula:
Em que:
E vamos ver que a melhor forma de determinarmos esses valores vai ser sendo só rotacionar as seções, o que torna tudo mais tranquilo.
E por fim, ainda temos que determinar o ângulo que a LN faz com a horizontal, e para isso usaremos a seguinte conta:
Ou seja, precisamos seguir um passo a passo para podermos determinar as tensões, então vamos lá:
Primeiro temos que determinar os momentos em cada uma das direções, ou seja, vamos abrir os momentos fletores em cada uma das direções, e depois analisamos cada uma das direções, sendo assim teremos que:
Decompondo os momentos fletores teremos que:
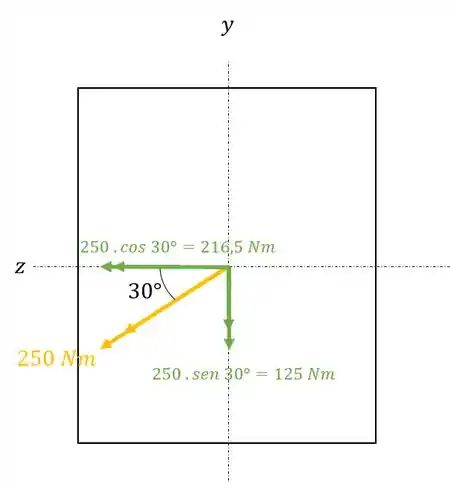
Agora que já temos os momentos fletores em cada direção, podemos analisar cada uma delas separadamente.
Passo 2
Como a seção é simétrica, não precisamos determinar a LN, porque ela já vai estar no meio das seções, então precisamos determinar os momentos de inércia e as distancias em y e em z, olhando cada direção teremos que:
Olhando a seção Z apenas com o momento nessa direção teremos que:
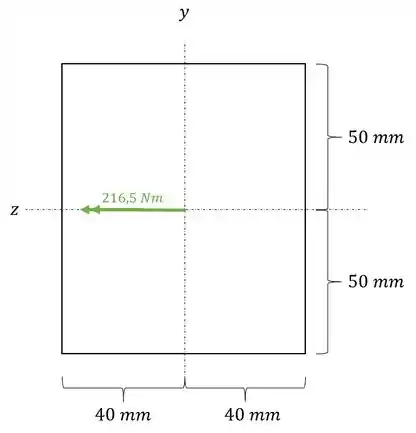
Nessa seção temos que determinar as tensões no ponto A e B, e para isso precisamos do valor de y, sendo assim teremos que:
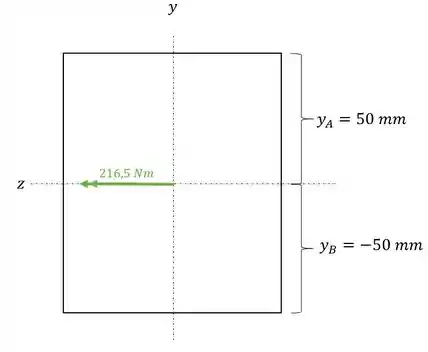
E com isso podemos determinar uma parte da tensão máxima, já que podemos usar a seguinte parte da equação.
Com isso teremos que:
Agora vamos ao cálculo na outra direção.
Olhando a seção y apenas com o momento nessa direção teremos que:
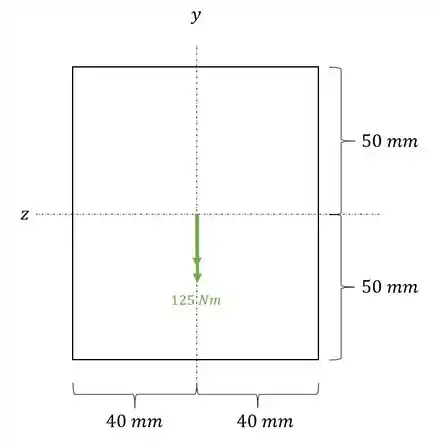
Agora temos que tomar um cuidado, o momento de inércia é na direção y, certo? Ou seja, na nossa fórmula de momentos de inércia, o B SEMPRE é paralelo ao eixo analisado, nesse caso o y, e H SEMPRE é perpendicular ao eixo analisado, que é o eixo y, sendo assim teremos que:
Nessa seção temos que determinar as tensões no ponto A e B, e para isso precisamos do valor de Z, sendo assim teremos que:
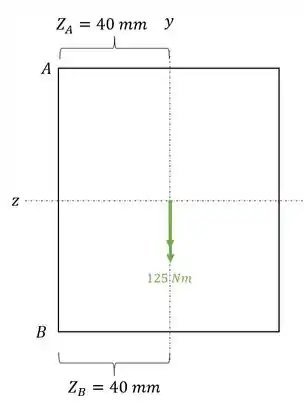
E com isso podemos determinar uma parte da tensão máxima, já que podemos usar a seguinte parte da equação.
Com isso teremos que:
E com isso podemos determinar a tensão total nos pontos A e B juntando as duas parcelas:
Sendo assim teremos que para o item a):
Sendo assim teremos que para o item b):
Passo 3
E agora para o item c) devemos usar a seguinte equação: