Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 44
Usando , determinar a energia de deformação devido à flexão, para a viga com o carregamento mostrado (desprezar o efeito das tensões de cisalhamento).
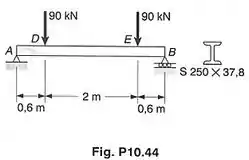
Passo 1
Ei, você aí! Você mesmo! Pronto para mais uma questão de energia de deformação?
Nesse exercício precisamos calcular a energia de deformação da barra . Nesse exercício vamos calcular apenas a energia de deformação da barra que é causada pelo momento fletor presente na barra. A equação que calcula essa energia da barra causada pelo momento fletor é:
onde é o comprimento total da barra , é o módulo de elasticidade e é o momento de inércia.
Para calcular o momento fletor , temos que achar as forças que atuam na barra. A figura abaixo mostra as forças atuando na barra .
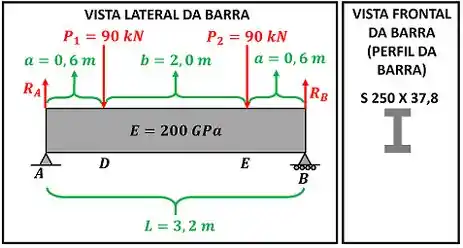
é a força de reação causada pela restrição no ponto e é a força de reação causada pela restrição no ponto . Elas são encontradas através das equações de equilíbrio de forças em . No próximo passo, calcularemos essas duas forças!
Passo 2
Para achar e através do equilíbrio de forças em , precisamos notar que essa barra é simétrica! Isso significa que a força de reação da ponta esquerda da barra e a força de reação da ponta direita da barra são iguais!
Como as forças e da barra estão para baixo, elas ganham um sinal de menos na equação de equilíbrio em .
Além disso, precisamos lembrar que as forças e de vale .
Como é igual a :
Agora estamos aptos a achar !
Passo 3
Para achar precisamos usar a equação de equilíbrio de momento na parte esquerda da barra . Calcularemos o equilíbrio no ponto . O momento tem três valores: um quando a parte esquerda da barra ainda não inclui as forças e . Outro quando a parte esquerda inclui a força . O último quando a parte esquerda inclui as forças e . Vamos começar o cálculo do primeiro valor de .
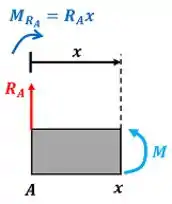
Como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Agora vamos calcular o segundo valor de .
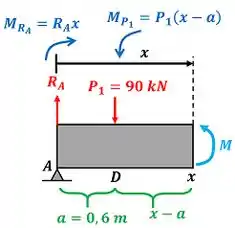
De novo precisamos observar que, como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Por fim, vamos calcular o terceiro valor de .
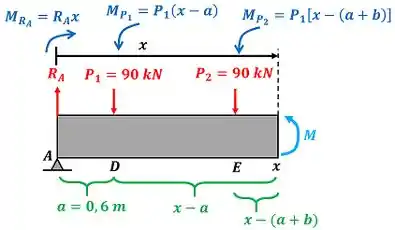
De novo (que saco, né?) precisamos observar que, como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Com esses valores de , podemos achar !
Passo 4
tem dois valores. Um quando vale entre e , outro quando vale entre e e o terceiro quando vale entre e
Por isso, para substituir na integral que calcula , precisamos separar a integral em duas. Uma que vai de a para o primeiro valor de , outra que vai de a para o segundo valor de e a última que vai de a .
Agora, temos que substituir os valores de , e nas integrais corretas.
Antes disso, temos que converter o módulo de elasticidade de para , multiplicando por .
O momento de inércia do perfil da barra pode ser encontrado no apêndice C para o perfil S 250 X 37,8. Na tabela do apêndice C, o valor de está em . Para converter esse valor para , precisamos multiplicar por .
Pronto, enfim podemos usar a integral para calcular .
Colocando as constantes para fora da integral, achamos: