Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 185
Sabendo-se que e , selecionar o perfil de abas largas que poderá ser usado para suportar o carregamento mostrado.
Passo 1
Fala aí galera do Responde aí.
Para essa questão, devemos calcular o diagrama de esforços para acharmos a maior tensão. Com isso, relacionamos ela com os dados da seção para achar o melhor perfil.
Primeiramente, vamos obter as reações de apoio:
Agora, vamos fazer os diagramas:
Diagrama de cortante:
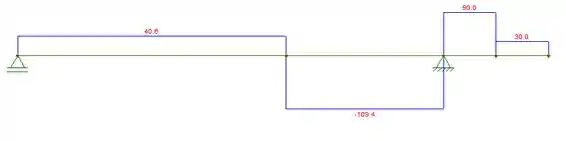
Diagrama de momento fletor:
Passo 2
Agora, basta substituir nas fórmulas da tensão. As tensões são dadas por:
Como o perfil é de aba largas, a espessura das abas é desprezível e portanto, a área das abas também. Logo:
Onde é a distância entre as abas e a espessura.
Substituindo:
Temos 2 incógnitas e 2 equações. Logo:
Resposta
Exercícios de Livros Relacionados
Determinar: a) Intensidade P de duas forças, dirigidas de baixo para cima, para que o máximo valor absoluto do momento fletor na viga seja tão pequeno quanto possível; b) a correspondente tensão norma
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar o máximo valor absoluto a) força cortante b) momento fletor.
Determinar as equações das curvas dos diagramas de força cortante e de momento fletor, para a viga com o carregamento mostrado. Determinar o máximo valor absoluto do momento fletor na viga.
Para a viga com o carregamento mostrado, determinar: a) máximo valor absoluto do momento fletor b) máxima tensão normal devido à flexão.
Para a viga com o carregamento mostrado, determinar: a) o máximo valor absoluto d momento fletor b) maior tensão normal devido à flexão.