Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 165

Usando o método dos nós, determine a força em cada elemento da treliça de passo duplo mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.

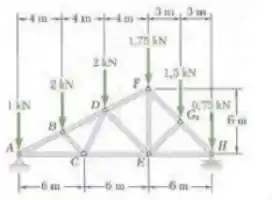
Passo 1

Antes de calcular cada nó, vamos calcular as reações dos apoios em A e H utilizando as condições de equilíbrio. Assim, teremos

∑ M a = 0 →

H ⋅ 18 m - 2 k N ⋅ 4 m - 2 k N ⋅ 8 m - 1.75 k N ⋅ 12 m - 1.5 k N ⋅ 15 m - 0.75 k N ⋅ 18 m = 0

H = 4.5 k N   p a r a   c i m a

∑ F x = 0 → 0 → A x = 0

∑ F y = 0 → A y + H - 9 = 0 → A y = 4.5 k N   p a r a   c i m a

Agora, vamos analisar cada um dos nós começando pelo nó A , teremos então

F a b 5 = F a c 2 = 3.5 k N 1 → F a b = 7.83 k N   c o m p r e s s ã o e   F a c = 7.0 k N ( t r a ç ã o )

Passo 2

Seguindo com a análise dos nós vamos para o nó B

∑ F x = 0 → 2 5 ⋅ F b d + 2 5 ⋅ 7.8262 k N + 1 2 ⋅ F b c = 0   i

∑ F y = 0 → 1 5 ⋅ F b d + 1 5 ⋅ 7.8262 k N - 1 2 ⋅ F b c - 2 k N = 0   i i

Fazendo 2 ⋅ i + i i teremos

3 F b d = - 19.0065 → F b d = - 6.3355 k N   c o m p r e s s ã o

Fazendo, agora, i i - i obtemos

2.3711 ⋅ F b c = - 4.4721 → F b c = - 1.8861 k N   c o m p r e s s ã o

Para o nó C vamos ter

∑ F y = 0 → 2 5 ⋅ F c d - 1 2 ⋅ 1.8861 k N = 0 → F c d = 1.491 k N   t r a ç ã o  

∑ F x = 0 → F c e - 7 k N + 1 2 ⋅ 1.8861 k N + 1 5 ⋅ 1.4911 k N = 0

F c e = 5 k N   ( t r a ç ã o )

Para o nó D teremos

∑ F x = 0 → 2 5 ⋅ F d f + 1 2 ⋅ F d e + 2 5 ⋅ 6.3355 k N - 1 5 ⋅ 1.4911 k N = 0

→ F d f + 0.79057 F d e = - 5.59 k N       i

∑ F y = 0 → 1 5 ⋅ F d f - 1 2 ⋅ F d e + 1 5 ⋅ 6.3355 k N = 2 5 ⋅ 1.4911 k N - 2 k N = 0

→ F d f - 0.79057 F d e = - 1.1188 k N   i i

Somando ( i ) com ( i i ) teremos

2 F d e = - 6.7088 k N → F d f = - 3.3544 k N   c o m p r e s s ã o

Subtraindo i i de i temos

1.58114 F d e = - 4.4712 k N → F d e = - 2.8278 k N   c o m p r e s s ã o

Passo 3

Calma que já estamos terminando, faltam só mais 3 nós. Indo, então, para o nó F teremos

∑ F x = 0 → 1 2 ⋅ F f g + 2 5 ⋅ 3.3544 k N = 0

→ F f g = - 4.243 k N   c o m p r e s s ã o

∑ F y = 0 →   - F e f - 1.75 k N + 1 5 ⋅ 3.3544 k N - 1 2 ⋅ - 4.243 k N = 0  

F e f = 2.75 k N   t r a ç ã o

Agora analisaremos o nó G

∑ F x = 0 → 1 2 ⋅ F g h - 1 2 ⋅ F e g + 1 2 ⋅ 4.243 k N = 0

→ F g h - F e g = - 4.243 k N   i

∑ F y = 0 →   - 1 2 ⋅ F g h - 1 2 ⋅ F e g - 1 2 ⋅ 4.243 k N - 1.5 k N = 0

→ F g h + F e g =   - 6.364 k N     i i

Somando as duas equações obtemos

F g h = - 10.607 k N 2 = - 5.303 k N   c o m p r e s s ã o

Substituindo esse valor em qualquer uma das equações vamos encontrar

2 F e g = - 2.121 k N → F e g = - 1.0605 k N   c o m p r e s s ã o

E finalmente vamos analisar o último nó que é o nó H . Assim, obteremos

F e h 1 = 3.75 k N 1 → F e h = 3.75 k N   t r a ç ã o

F g h 2 = 3.75 k N 1 → F g h = 5.3 k N   c o m p r e s s ã o

Resposta

F a b = 7.83 k N   c o m p r e s s ã o e   F a c = 7.0 k N ( t r a ç ã o )

F b d = 6.34   k N   c o m p r e s s ã o   e   F b c = 1.8861 k N   c o m p r e s s ã o

F c d = 1.491 k N   t r a ç ã o     e   F c e = 5 k N   ( t r a ç ã o )  

F d f = 3.35 k N   c o m p r e s s ã o   e   F d e = 2.83 k N   c o m p r e s s ã o

F f g = 4.24 k N   c o m p r e s s ã o   e   F e f = 2.75 k N   t r a ç ã o

F g h = 5.3 k N   c o m p r e s s ã o   e     F e g = 1.061 k N     c o m p r e s s ã o

F e h = 3.75 k N   t r a ç ã o   e   F g h = 5.3 k N   c o m p r e s s ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

59. Uma treliça de telhado tipo Polinésia ou dupla inclinação é carregada como mostrado na figura. Determine a força nos elementos, D F ,E F e E G .
60. Uma treliça de telhado tipo Polinésia ou dupla inclinação é carregada como mostrado na figura. Determine a força nos elementos, H I ,G I e G J .
42. A treliça mostrada na figura consiste em 18 elementos e é sustentada por uma rótula em A , duas pequenas hastes de conexão em B e uma pequena haste de conexão em G . ( a ) Verifique se essa treliç
39. A treliça mostrada na figura consiste em nove elementos e é sustentada por uma rótula em B , uma pequena haste de conexão em C e por duas pequenas hastes em D . ( a ) Verifique se essa treliça é u
40. Resolva o Problema 6.39 para P = 0 e Q = (- 900 N) k