Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 68
68. Determine as reações em e quando :
Passo 1
Bom! Como é um membro que está submetido a duas forças, a força exercida no membro é direcionada ao longo do segmento . Baseado nisso, façamos o esboço do sistema , considerando o sistema de três forças que nele estará presente:
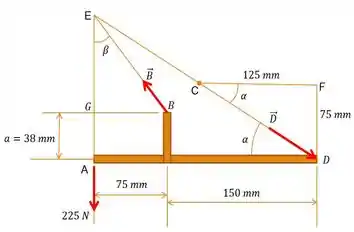
E em seguida, calculemos a tangente de no triângulo :
E depois, calculemos o valor de no triângulo :
Com isso, o valor de é:
E para o triângulo , uma vez que sabemos o valor de calculemos a tangente de :
Passo 2
Agora que já sabemos o valor do ângulo e do ângulo , vamos fazer o triângulo de forças para o nosso sistema com as forças , e de :
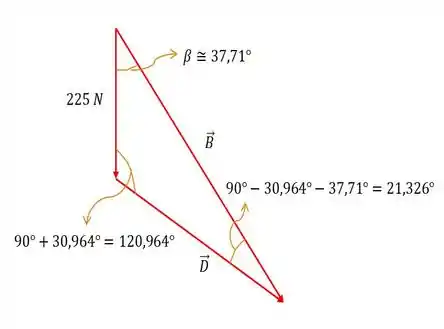
E para achar o valor das forças e , basta usar a lei dos senos:
Primeiro para a força em :
E depois para a força em :
Ah!! E antes que alguém pergunte onde está a força ; é só dar uma olhadinha na figura do . Com isso, veremos que é um membro que está submetido a duas forças, que no caso, serão iguais. Logo é igual a :