Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 88
Usando o método do trabalho e energia, resolver o Prob. 3.34.
Passo 1
Oi, pessoal! Como vão? Partiu fazer uma questão de cálculo de ângulo de rotação da torção através do método de energia pra arrasar na prova?
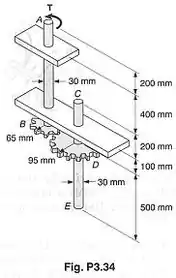
Essa questão mostra um eixo sendo torcido com um torque . Esse torque faz os eixos e absorverem uma energia total e se deformarem. O enunciado pede que a gente ache o ângulo de rotação da extremidade do eixo, usando duas equações para calcular a energia absorvida pelos eixos e . A primeira, calcula a partir do torque .
A segunda equação, calcula somando a energia absorvida pelo eixo com a energia absorvida pelo eixo .
Para calcular e usamos a equação 10.22 do livro que calcula a energia absorvida por um eixo em torção.
é o módulo de elasticidade transversal do material das barras que vale . e são os comprimentos das barras e respectivamente.
Para fazer esses cálculos, supomos que as duas barras estão girando tão devagar que estão em equilíbrio! A figura abaixo mostra os dados que temos para achar .
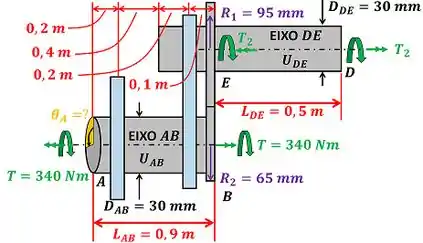
e são os diâmetros das barras e respectivamente. e são os raios da engrenagem da barra e respectivamente.
Agora que temos todas essas fórmulas, vamos começar a fazer as contas, calculando o valor do torque !
Passo 2
Para achar o torque temos que lembrar da terceira lei de Newton chamada de ação e reação. Levando essa lei em conta, vemos que a engrenagem da barra empurra a engranagem da barra com uma força e a engrenagem da barra reage empurrando a engrenagem da barra com uma força igual e oposta!
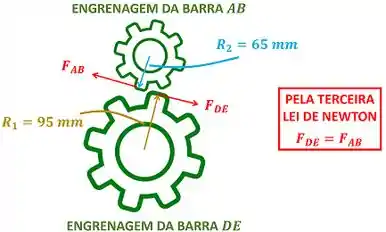
Como os torques são iguais às forças divididas pelos raios , concluímos que:
Agora só falta achar os momentos de inércia polares e para a gente calcular e .
Passo 3
Antes de achar as energias de deformação e de cada barra, temos que encontrar os valores dos momentos de inércia polares e de cada barra
Achamos e , através das fórmulas de momentos de inércia polares para áreas circulares abaixo. Antes, devemos converter os diâmetros de pra , multiplicando eles por .
Com esses valores podemos partir para nosso passo final!
Passo 4
Substituímos e nas equações de e para achar as energias de deformação. No entanto, antes disso converter o de para , multiplicando por .
Somando com , achamos .
Substituindo esse valor na fórmula de , achamos:
Para converter esse valor de ângulo de radiano para grau, multiplicamos ele por e dividimos por .
Show de bola! Finalizamos com a questão! Vamos tirar 10 na prova! :-D