Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 72
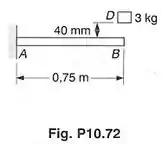
O bloco é abandonado da posição mostrada, sobre a extremidade de uma barra de aço quadrada, de de lado. Sabendo-se que , determinar na barra:
- a máxima deflexão em sua extremidade livre;
- o máximo momento fletor;
- a máxima tensão normal.
Passo 1
Como estão, queridos e queridas? Bora resolver uma questão de carregamento produzido por impacto para diminuir as dúvidas sobre esse tópico?
A questão quer saber três informações:
- A máxima deflexão no ponto . Ela é a deformação provocada na barra as com o choque choque do bloco. Calculamos através da energia que a barra absorve no impacto. A energia é calculada pela equação abaixo que depende de .
- O máximo momento fletor é encontrado através do equilíbrio de momentos da viga.
- Para encontrar a maior tensão na viga, aplicamos a equação da tensão máxima de barras em flexão presente abaixo.
onde é a força que provoca na barra as mesmas tensões produzidas pelo choque. Além disso, a energia que a barra absorve é igual à energia potencial transferida do bloco para a barra no momento do choque.
Igualando essas duas equações e encontrando uma equação para em função de no apêndice , conseguimos achar .
Os dados que temos para achar , e se encontram na figura abaixo.
e são a altura e a largura do perfil da viga respectivamente.
Após entender tudo isso, podemos calcular no próximo passo.
Passo 2
A primeira etapa para encontrar é igualar as duas equações de .
A segunda etapa é deduzir uma fórmula de em função de a partir da equação de presente no apêndice .
Substituindo essa fórmula de na equação anterior, achamos:
A equação acima, mostra que para achar , precisamos achar a raiz positiva do polinômio do segundo grau através da fórmula de Bhaskara. No entanto, para achar a raiz, precisamos achar os valores numéricos dos coeficientes do polinômio. Para isso, precisamos descobrir quanto vale o momento de inércia do perfil através de para perfis quadrangulares abaixo.
Antes de substituir os dados na equação, precisamos converter de pra multiplicando por e converter de pra multiplicando por .
Pelo polinômio acima nós vemos que os coeficientes dele são:
Sabendo disso, somos capazes de calcular por Bhaskara.
Ebaaaa! Lutamos, mas conseguimos resolver a letra (a) da questão! Vamos partir pra letra (b) agora!
Passo 3
Para achar a tensão , temos que achar primeiro. Para achr precisamos encontar a força . Fazemos isso, substituindo o valor de na fórmula de deduzida a partir das informações extraídas no apêndice .
Agora, podemos achar o máximo momento fletor , fazendo o equilíbrio de momentos da viga em relação ao ponto .
Fazer o equilíbrio de momento em relação ao ponto é a mesma coisa que dizer que a soma dos momentos em relação a vale zero.
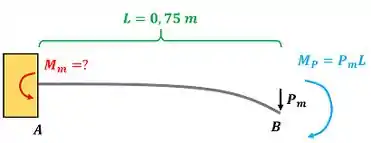
Para fazer esse equilíbrio e achar , temos que ter atenção nos sinais do momento! Como o momento tende a girar a viga no sentido horário, temos que colocar um sinal de menos na frente dele!
Isso aííí! Encontramos o momento fletore máximo e resolvemos a letra (b) da questão!
Essa é a primeira etapa para achar . Vamos deixar a última etapa para o próximo passo!
Passo 4
Antes de substituir na equação de , temos que achar a distância entre o ponto de maior tensão no perfil da viga e o centro da viga. é igual à metade da altura do perfil da viga.
Substituindo os dados na equação de , achamos:
Pronto! A letra (c) da questão também está feita! Acabamos tudo! Uhuul!