Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 78
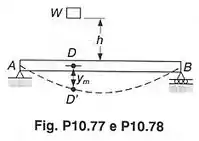
Um bloco de peso é abandonado de uma altura acima de uma viga horizontal e choca-se com elas no ponto . Pede-se:
- Denotando por o valor exato da máxima deflexão em , e por o valor obtido desprezando-se o efeito dessa deflexão na variação da energia potencial do bloco, mostrar que valor absoluto do erro relativo nunca excede a ;
- verificar o resultado obtido na parte a, resolvendo a parte a do Prob. 10.72, sem levar em conta , na determinação da variação de energia potencial da carga. Comparar a resposta obtida por este caminho com a exata resposta daquele problema.
Passo 1
E aí, galerinha! Estudando muito? Bora fazer um exercício de carga produzida por choque?
Na letra (a), o enunciado quer que a gente calcule o erro relativo que ocorre, quando consideramos que a energia potencial que a barra absorve não leva em conta a deflexão que a barra sofre. Nesse caso (caso 1), a energia potencial que a barra absorve do bloco vale:
Devemos comparar a deformação que a barra sofre, quando absorve essa energia potencial com a deformação que a barra sofre, quando ela absorve uma energia potencial . Nesse caso 2, o cálculo de leva em conta a deflexão que a barra sofre.
Depois de achar e devemos calcular o erro relativo pela equação abaixo e mostrar que ele é sempre menor ou igual a .
onde as barrinhas ao redor de são o módulo (valor absoluto sem sinal) desse termo.
A figura abaixo mostra esses dois casos.
Já na letra (b), o enunciado quer que a gente calcule o erro relativo do Prob. 10.72, lembrando que, para esse problema (calculado no Prob 10.72).
O do Prob 10.72 é encontrado a partir da equação presente no apêndice do livro.
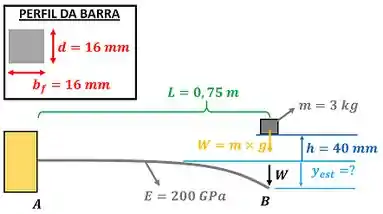
A figura abaixo mostra os dados da questão 10.72.
No próximo passo vamos começar as contas determinando o valor de da letra (a).
Passo 2
Para encontrar , temos que lembrar que podemos calcular a energia através da força que o bloco exerce sobre a viga, quando se choca com ela.
Substituindo essa equação na outra equação de , obtemos.
A equação resultante mostra que só falta achar uma equação de em função de para achar .
Achamos essa equação no apêndice do livro.
onde é o módulo de elasticidade do material da vida e é o momento de inércia do perfil da viga.
Agora, vamos substituir na equação de que deduzimos.
Agora só falta achar para calcular o erro relativo .
Passo 3
Calculamos através do mesmo passo a passo que usamos para .
Primeiro, lembramos que podemos calcular a energia através da força que o bloco exerce sobre a viga, quando se choca com ela.
Substituindo essa equação na outra equação de , obtemos.
A equação resultante mostra que só falta achar uma equação de em função de para achar .
Mais uma vez temos que recorrer ao apêndice do livro para achar uma equação.
No entanto, podemos achar o valor de reorganizando a equação de .
Logo, vale:
Agora, vamos substituir na equação de que deduzimos.
Dividindo todos os termos por e multiplicando todos os termos por , achamos:
Colocando em evidência e jogando pro outro lado da equação:
Podemos lembrar dos produtos notáveis, para reduzir .
O módulo do lado esquerdo da equação deve excluir o sinal de menos que tem na frente de .
Como é igual a :
é maior ou igual a , porque a deflexão é gerada quando a viga absorve mais energia potencial. Isso gera um deslocamento maior da viga. Logo:
Ou seja:
Aeeeeee! Mostramos o que a letra (a) da questão queria!
Passo 4
Agora temos que resolver a letra (b) da questão, calculando o do Prob. 10.72.
A única variável presente na equação do que não conhecemos é o da viga. Calculamos esse valor, lembrando que podemos calcular a energia através da força que o bloco exerce sobre a viga, quando se choca com ela.
Substituindo essa equação na outra equação de , obtemos.
A equação resultante mostra que só falta achar uma equação de em função de para achar .
Achamos essa equação no apêndice do livro.
Agora, vamos substituir na equação de que deduzimos.
é o módulo de elasticidade do material da viga que vale , é o comprimento da viga que vale e é o momento de inércia da viga que pode ser calculado pela equação de momento de inércia para perfis quadrangulares abaixo.
é o peso do bloco.
Substituindo tudo isso na equação de , achamos:
Substituindo esse valor na equação do erro relativo .
Acaboooou! Encontramos o que a letra (b) da questão pedia, verificando a fórmula que deduzimos na letra (a)!