Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 95
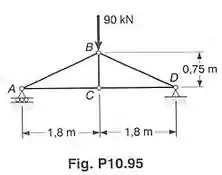
Cada membro da treliça mostrada é feito de aço e tem uma seção transversal de área igual a . Usando-se , determinar a deflexão vertical do ponto , provocada pela carga de .
Passo 1
Faaaala, galerinha! Prontos para uma questão de cálculo de deflexão através do método de energia?
O enunciado mostra uma figura com 5 membros da treliça (, , , e ) e quer que a gente calcule a deflexão do ponto produzida pela força que é aplicada em .
Como temos que usar o método da energia, vamos calcular a partir da equação que calcula a quantidade de energia que é absorvida pela treliça, quando ela se deforma.
é a energia total absorvida pela treliça. Logo, é a soma das energias absorvidas por cada treliça. Isso é mostrado pela equação abaixo.
Para calcular cada uma dessas energia, vamos precisar calcular as forças aplicadas a cada um dos membros da treliça! A figura abaixo mostra as forças que são aplicadas a cada membro mais a força . Atenção! Essas não são todas as forças que existem no problema. Elas são apenas as forças que entrarão no cálculas das energias mais a força .
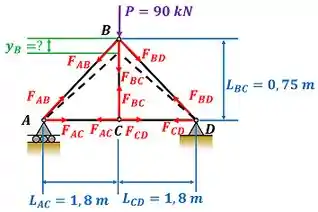
Para encontrar as energias de cada membro da treliça, usaremos a equação 10.14 que calcula a energia absorvida por uma barra de comprimento , quando ela sofre a ação de uma força axial .
Agora podemos começar os cálculos no próximo passo.
Passo 2
Para encontrar as forças , , , e , precisamos calcular a reação da restrição do ponto e a reação do ponto .
Para fazer esses cálculos, vamos usar o diagrama de corpo livre da treliça inteira abaixo.
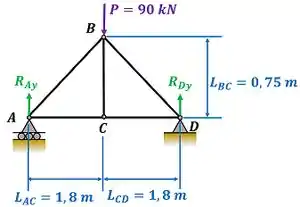
Primeiro, vamos fazer o equilíbrio de forças na treliça inteira. Esse equilíbrio diz que a soma de todas as forças em vale zero. Como a força está apontando pra baixo, ela ganhará um sinal de menos na equação. Além disso, vemos que a treliça e as forças são simétricas. Logo, é igual a .
Pronto! Achamos todas as reações! Agora somos capazes de achar as forças , , , e aplicadas nos membros da treliça.
Passo 3
Para facilitar nossa vida na hora de achar essas forças, podemos observar novamente que as forças e a treliça são simétricas. Por isso:
Agora, podemos achar e , fazendo o equilíbrio de forças no ponto .
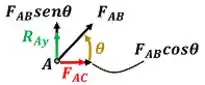
O equilíbrio de forças em resulta em:
Já o equilíbrio em leva ao resultado abaixo.
Agora podemos achar a força restante, fazendo o equilíbrio das forças em do ponto .
Temos que lembrar antes, que no equilíbrio em , todas as forças apontando pra baixo ganham um sinal de menos na frente.
Para achar o e o e conseguir calcular o valor das forças, recorremos ao desenho abaixo. Nele, vemos que foi calculado usando o teorema de Pitágoras com e de catetos.
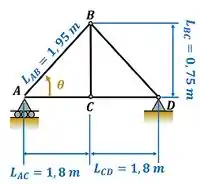
Substituindo nas equações das forças:
Agora podemos achar as energias de cada membro da treliça.
Passo 4
Para achar as energias , , , e dos membros, usamos as forças que calculamos na equação de energia do passo 1.
Antes, precisamos converter de pra multiplicando por , converter de pra multiplicando por e converter de pra multiplicando por .
Com esse valores, podemos calcular e no próximo passo.
Passo 5
Somando todas as energias de cada membro da treliça, achamos .
é encontrado a partir da fórmula que deduzimos no passo 1.
Boooooa, meus queridos! Chegamos na resposta da questão!