Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 145

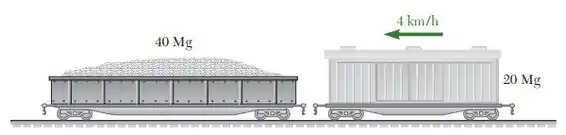
Um vagão ferroviário de 20 Mg movendo a 4 km/h é acoplado a um vagão ferroviário de 40 Mg que está em repouso com as rodas travadas ( μ k = 0,30 ). Determine (a) a velocidade dos carros depois que acoplamento for completado, (b) o tempo que os carros levam para ficar em repouso.

Passo 1

Vamos resolver uma questão que parece ser difícil, mais é simples. Para determinar a velocidade dos carros depois do acoplamento vamos partir da conservação da quantidade de movimento. Assim temos:

∑ m v i n i c i a l = ∑ m v f i n a l

No início, tratamos cada carro separado. Após o acoplamento, tratamos que os carros estão juntos. Dessa forma:

m A v A + m B v B = m A + m B v '

40 ⋅ 0 + 20 ⋅ 4 = 20 + 40 v '

v ' = 1,33 3   k m / h

Passo 2

Agora, para calcular o tempo que os carros, depois de acoplados, demoram para ficar em repouso, vamos usar o princípio do impulso. Vamos observar o diagrama de corpo livre para os carros:

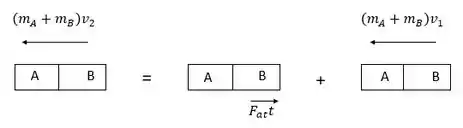
O impulso é ocasionado pela força de atrito das rodas do carro A, que provoca a desaceleração dos carros. Assim temos:

I m p =   - μ k N t =   - μ k m A g t

E a velocidade inicial é:

v 1 = v '

Passo 3

Substituindo na equação do princípio de impulso:

m A + m B v 1 - μ k m A g t = m A + m B v 2

60000 1,333 3,6 - 0,30 ⋅ 4 0000 ⋅ 9,81 ⋅ t = 0

t = 0,1888   s

Resposta

  1. 1,333 km/h
  2. 0,1888 s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma criança de massa 22 kg está sentada em um balanço e sendo mantida na posição mostrada na figura por uma segunda criança. Desprezando o peso do balanço, determine a tração no cabo AB (a) enquanto a
Os blocos A e B pesam 20 lb cada, o bloco C pesa 14 lb e o bloco D pesa 16 lb. Sabendo que uma força descendente de magnitude 24 lb é aplicada ao bloco D, determine (a) a aceleração de cada bloco, (b)
Uma esfera D de 100 g está em repouso em relação a um tambor que gira a uma taxa constante. Desprezando o atrito, determine o intervalo admissível da velocidade v da esfera se nenhuma das forças exerc
No Problema 12.63, determine o menor valor permitido da razão die em termos de e , m , v 0 e V se em x = l, a distância mínima permitida entre o caminho dos elétrons e a placa positiva é 0,05d.12.63 -
No tubo de raios catódicos mostrado, os elétrons emitidos pelo cátodo e atraídos pelo ânodo passam por um pequeno orifício no ânodo e viajam em linha reta com uma velocidade vo até atingirem a tela em