Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 191

Um vagão ferroviário de massa m e velocidade inicial v colide e se acopa com os dois vagões idênticos. Calcule a velocidade final v ' do grupo de três vagões e a fração n de perda de energia se (a) a distância de separação inicial d = 0 (isto é, os dois vagões estacionados estão inicialmente acoplados sem folga no engate) e (b) a distância d ≠ 0 de modo que os vagões estão desacoplados e ligeiramente separados. Despreze a resistência ao rolamento.

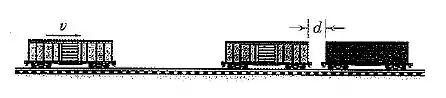
Passo 1

(a) Vamos lembrar da lei de conservação de momento linear:

p i = p f

Inicialmente só o vagão da esquerda tem momento diferente de zero, e após a colisão o conjunto de três vagões se move junto com velocidade v ' :

m v = 3 m v '

v ' = m 3 m   v

v ' = 1 3   v

Passo 2

(a) E qual é a perda de energia nesse mesmo processo?

Δ E = 1 2 m v 2 - 1 2 3 m v ' 2

Δ E = 1 2 m v 2 - 1 2 3 m 1 3 v 2

Δ E = 1 2 - 1 6 m v 2 = 1 3 m v 2

E a perda em relação à energia inicial é:

n = Δ E K i = 1 3 m v 2 1 2 m v 2 = 2 3

Passo 3

(b) E agora, o que muda no caso em que d ≠ 0 ? Absolutamente nada! Vamos mostrar isso para garantir.

Dessa vez teremos duas colisões. A primeira acontece entre os dois primeiros vagões, que passam a andar juntos com uma velocidade intermediária v i n t :

p i = p f

m v = 2 m v i n t

v i n t = 1 2 v

E a segunda colisão acontece entre esse par de vagões com velocidade v i n t e o terceiro. Depois da colisão o conjunto de três vagões passa a andar com velocidade v ' :

p i = p f

2 m v i n t = ( 3 m ) ( v ' )

2 m 1 2   v = ( 3 m ) ( v ' )

v ' = 1 3   v

Ou seja, chegamos no mesmo resultado de antes! Naturalmente, isso quer dizer que o cálculo da perda de energia dará o mesmo resultado.

Resposta

Nos dois casos a velocidade final é v ' = 1 3 v e a perda de energia é de 2 3 da energia inicial.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

142 A escavadeira carrega inicialmente 10 m 3 de areia com uma densidade de 1520 kg/ m 3 . A areia é descarregada horizontalmente através de uma portinhola P, de 2,5 m 2 , a uma taxa de 900 kg/s, medi
139. Um foguete vazio tem uma massa de 250 Kg e carrega 150Kg de combustível. Se o combustível é queimado a uma taxa de 7,5 kg/s e ejetado a uma velocidade de 1320 m/s, em relação ao foguete, determin
130. O segundo estágio B do foguete de dois estágios tem uma massa de 5Mg (vazio) e é lançado a partir do primeiro estágio A com uma velocidade inicial de 600 Km/h. O combustível do segundo estágio te
133. O caminhão tem massa de 50Mg quando está vazio. Quando está descarregado 5 m 3 de areia a uma taxa constante de 0,8 m 3 s , a areia flui para fora a uma velocidade de 7m/s, medida em relação ao c
138. O vagão é usado para coletar água acumulada em uma calha nos trilhos. Determine a forca necessária para impelir o vagão a uma velocidade constanve v, para cada um dos três casos. O coletor tem um