O ônibus espacial lança um satélite de ejetando-o a partir do compartimento de carga como mostrado. O mecanismo de ejeção é ativado e permanece em contato com o satélite por para fornecer uma velocidade de na direção em relação ao ônibus espacial. A massa do ônibus espacial é de . Determine a componente da velocidade do ônibus espacial no sentido negativo da direção resultante da ejeção. Encontre também a média no tempo da força de ejeção.
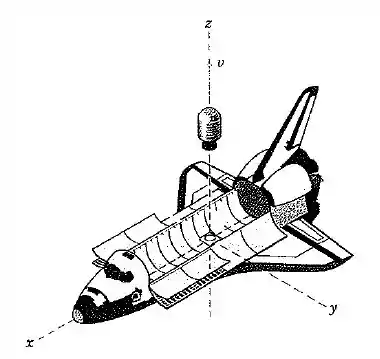
Passo 1
Podemos considerar que o conjunto formado pelo satélite e pelo ônibus espacial é um sistema fechado, ou seja, o momento linear total desse conjunto tem que permanecer constante!
Além disso, precisamos ter cuidado porque a velocidade dada no enunciado () é relativa entre o satélite e o ônibus.
Passo 2
Agora vamos considerar a conservação de momento linear na direção . Antes de o ônibus lançar o satélite não havia nenhum movimento nessa direção, então:
Em seguida, o satélite adquire uma velocidade e consequentemente o ônibus espacial adquire uma velocidade .
Onde estamos considerando o sentido positivo como vertical para cima (sentido positivo de na figura). Então ficamos com um sistema de equações:
Passo 3
Então vamos resolver esse sistema. Primeiro precisamos substituir os valores numéricos:
Eliminando entre as duas equações:
E agora temos que projetar essa equação no eixo , isso quer dizer que vamos fazer o produto escalar da equação pelo vetor unitário .
E esse último resultado é negativo porque o ônibus adquire velocidade vertical para baixo:
Passo 4
E agora queremos calcular a força média de ejeção. Vamos aplicar o teorema do impulso sobre o ônibus espacial.
Essa força, realizada na vertical para cima sobre o satélite tem uma reação vertical para baixo sobre o ônibus, e faz sua velocidade ir de até , então:
E esse é o módulo da média da força de ejeção.
Resposta
A velocidade do ônibus no sentido negativo é e a força média da ejeção é .