0 vento exerce uma força uniformemente distribuída de na superfície do painel
esquematizado na próxima figura. Reduza essa força à base da coluna de suporte desse painel
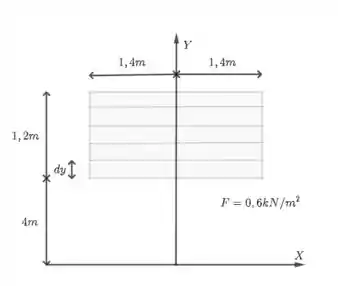
Passo 1
Vamos começar encontrando a força resultante. Para facilitar os cálculos, primeiro dividimos o painel em tiras de comprimento e altura , de modo que podemos tratar essas tiras como linhas.. Teremos uma força atuando em cada pequena seção de comprimento . Então, a força resultante em cada tira será
Para encontrar o ponto onde a força resultante deve ser aplicada, precisamos da integral
Logo, a força resultante deve ser aplicada no ponto , que corresponde ao centro da tira. O mesmo raciocínio é válido para todas as tiras. Então, a força atuando no painel é equivalente a uma força de módulo atuando na linha central do painel.
Passo 2
Temos novamente o problema de uma força uniformemente distribuída numa linha, mas agora em . Utilizando o mesmo raciocínio, encontramos
Então, a força aplicada uniformemente ao painel é equivalente a ter uma força de módulo atuando no ponto , que é justamente o ponto central do painel. A força resultante atua na mesma direção que a força uniformemente distribuída, ou seja, “entrando” no painel.
Passo 3
Para reduzir essa força resultante à base da coluna de suporte do painel, basta transladar a força resultante até a base da coluna. Devido a essa translação, temos que acrescentar um momento de módulo igual a multiplicação da força pela distância de translação. A força resultante estava atuando no ponto e é transladada para o ponto , o que significa que a distância de translação é . Logo, o momento induzido pela translação da força resultante tem módulo .
Resposta
,