O poste do exercício anterior é fixado na posição vertical com 15 por cento de seu comprimento dentro da base de concreto e solicitado através de um cabo que exerce uma força F em sua extremidade superior, como mostra a parte direita da figura. Reduza essa força ao nível do solo
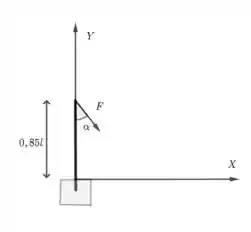
Passo 1
Como do comprimento poste está na base de concreto, então do nível do solo até a extremidade superior do poste, temos um comprimento de . Isso quer dizer que, no nosso sistema de coordenadas, a origem da força é o ponto . Nesse ponto, a força pode ser escrita como . Para reduzir essa força ao nível do solo mas ainda mantendo o mesmo efeito, temos que aplicar uma força e um momento nesse ponto. A força aplicada na origem será a força resultante, que nesse caso é o próprio . O momento da força será
Aqui, podemos ver que a translação do vetor ao nível do solo resultou em um momento de módulo igual ao produto da força pela distância de translação. O aparece porque apenas a componente horizontal da força terá contribuição.