Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 88

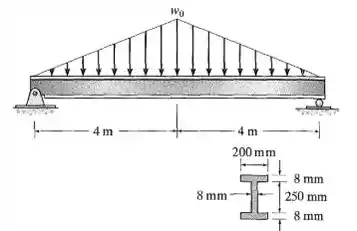
A viga de aço tem a área de seção transversal mostrada na figura. Determine a maior intensidade da carga distribuída w0 que ela pode suportar de modo que a tensão de flexão máxima na viga não ultrapasse σmáx = 150 MPa.

Passo 1

Primeiro, vamos calcular as reações:

∑ M a = 0 → 8 F b - 4 w 0 × 4 = 0

F b = 2 w 0

∑ F y = 0 → F a + 2 w 0 - 4 w 0 = 0

F a = 2 w 0

Vamos agora calcular o momento máximo, que fica no meio:

∑ M = 0 → M m á x + 2 w 0 × 4 3 - 2 w 0 × 4 = 0

M m á x = 16 w 0 3

Passo 2

Temos que calcular o momento de inércia:

I = 2 0,2 × 0,008 3 12 + 0,2 × 0,008 × 0,129 2 + 0,008 × 0,25 3 12 = 6,3685 × 10 - 5 m 4

A tensão máxima será dada por:

σ m á x = M c I

Isolando w0, teremos:

w 0 = 150 × 10 6 × 3 × 6,3685 × 10 - 5 16 × 0,133 = 13,47 k N / m

Resposta

w 0 = 13,47 k N / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob 4.80, considerando a viga do Prob 4.79
Para a viga do Prob 4.76, determinarO momento plástico M p O fator de forma da seção transversal
Para a viga do Prob 4.76, determinarO momento plástico M p O fator de forma da seção transversal
Resolver o Prob 4.80, considerando a viga do Prob 4.77
Determinar o momento plástico M p , para uma viga de aço de seção transversal mostrada, considerando o aço ser elastoplásticos, com tensão de escoamento igual a 300M P a