Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 86

A viga simplesmente apoiada é composta por quatro hastes de 16 mm de diâmetro, agrupadas como mostra a figura. Determine a tensão de flexão máxima na viga devido à carga mostrada.

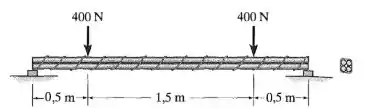
Passo 1

Por simetria, podemos ver que as reações valem 400N. Logo, podemos determinar o momento máximo (centro), que valerá:

M m á x = 400 × 2 - 400 × 1,5 = 200 N m

O momento de inércia será dado por:

I = 4 π 4 × 0,008 4 + π × 0,008 2 × 0,008 2 = 6,434 × 10 - 8 m 4

Passo 2

Podemos, então, determinar a tensão máxima:

σ m á x = 200 × 0,016 6,434 × 10 8 = 49,74 M P a

Resposta

σ m á x = 49,74 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga de seção transversal mostrada é feita de um aço que é considerado elastoplásticos com E = 200G P a e σ e = 240M P a . Por flexão em torno do eixo z, determinar o momento fletor e o raio de cu
Resolver o Problema 4.72, considerando que o momento de 150 Nm é paralelo ao eixo y
Uma viga de seção transversal mostrada é feita de um aço que é considerado elastoplásticos com E = 200G P a e σ e = 240M P a . Por flexão em torno do eixo z, determinar o momento fletor e o raio de cu
Uma viga de seção transversal mostrada é feita de um aço que é considerado ser elastoplásticos, com E=200GPa e σ e = 300M P a . Por flexão em torno do eixo z , determinar o momento fletor e o raio de
Uma viga de seção transversal mostrada é feita de um aço que é considerado ser elastoplásticos, com E=200GPa e σ e = 300M P a . Por flexão em torno do eixo z , determinar o momento fletor e o raio de