Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 139

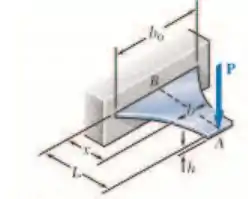
Uma viga em balanço AB consiste em uma placa de aço com altura uniforme h e largura variável a largura b feita para suportar a carga distribuída w ao longo de sua linha de centro AB. (a) Sabendo que a viga deve ter resistência constante, (b) Determine o valor máximo permitido de w se 0 L = 15 in.,b=8 in., h = 0,75 in., e σ= 24 ksi.

Passo 1

Fala aí gurizada tudo belezinha?? O exercício pede que a expresse b em função de x, L e b, então vem comigo :D, primeiramente vamos desenhar o diagrama de corpo livre :D

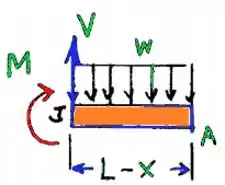
Vamos começar determinando o momento em J, vem comigo :D

∑ M =   F   x d = 0

M =   - w L - x 2 2

𝑂nde S é dado por:

S = M σ

Para uma seção transversal retangular

S = 1 6 b h ²

Igualando temos:

1 6 b h 2 = w L - x 2 2

Isolando b temos:

b o = 3 w L ² σ h ²

Passo 2

Gurizada agora podemos determinar o valor máximo permitido de w se 0 L = 15 in.,b=8 in., h = 0,75 in., e σ= 24 ksi

σ = M S = P x S

Para H temos:

w = σ b h 2 3 L 2 = 24 x 8 x 0,75 2 3 x 15 2 = 0,16   k i p / i n

Resposta

  1. b o = 3 w L ² σ h ²
  2. 0,16   k i p / i n
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força cortante e momento fletor e ( b ) do momento fletor.
Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força cortante e momento fletor e ( b ) do momento fletor.
Para a viga e carregamento mostrados, ( a ) trace os diagramas de força cortante e momento fletor e ( b ) determine as equações das curvas de força cortante e momento fletor.
Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força cortante e momento fletor e ( b ) do momento fletor.
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .