Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 9

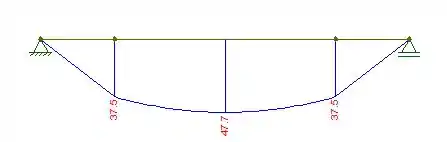
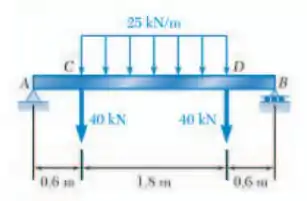
Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força cortante e momento fletor e ( b ) do momento fletor.

Passo 1

Fala aí galerinha, tudo bem? Bora zerar esse livro.

Para encontrarmos os diagramas de força cortante e momento fletor pedidos, precisamos esboçar o DCL do problema:

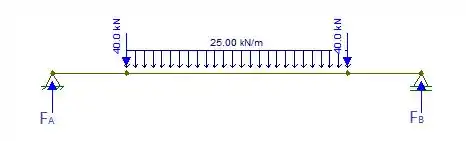
Primeiro, vamos usar as equações de equilíbrio para determinarmos as reações nos apoios, temos:

∑ M C = 0 - 40 0,6 - 45 1,5 - 40 2,4 + F B 3 = 0 F B = 62,5   k N

E também:

∑ F y = 0 F A + 62,5 - 40 - 45 - 40 = 0 F A = 62,5   k N

Com isso, a gente pode encontrar a força cortante e o momento fletor em cada ponto. Para o ponto C , temos:

∑ F y = 0 - 62,5 - V = 0 V = 62,5   k N

E para determinarmos a equação do momento fletor, temos:

∑ M 1 = 0 62,5   k N 0,6 + M = 0 M = - 37,5   k N

Passo 2

Em seguida, vamos utilizar as equações de equilíbrio novamente para determinarmos a força cortate e a equação de momento para ponto médio da viga. Para a equação de força cortante, temos:

∑ F y = 0 62,5 - 40 - 25 ( 0,9 ) - V = 0 V = 0

E também:

∑ M 2 = 0 62,5 1,5 - 40 0,9 + ( 25 ) ( 0,9 ) ( 0,45 ) - M = 0 M = - 47,7   k N ∙ m

Opa, com esses valores para a força cortante e momento fletor, podemos esboçar o diagrama para a força cortante. A gente não pode esquecer que nossa viga é simétrica, logo:

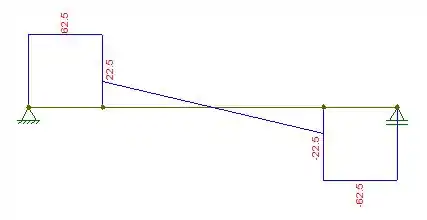
Agora que encontramos o diagrama para a força cortante, bora fazer o mesmo para o momento fletor:

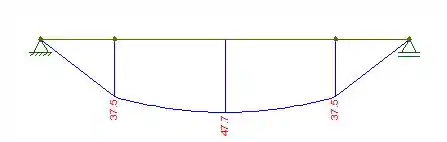
Com os diagramas, agora é só analisarmos o gráfico para encontrar os valores máximos da força cortante e momento fletor. Eles são dados por:

V m á x = 62,5   k N M m á x = 47,7   k N ∙ m

Isso é tudo, pessoal!!!

Resposta

V m á x = 62,5   k N M m á x = 47,7   k N ∙ m

Cortante:

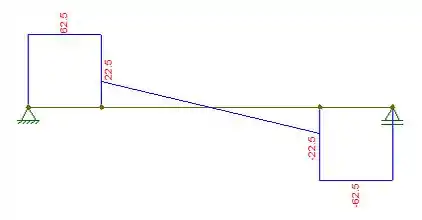
Momento:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a tensão de flexão máxima absoluta no eixo de 30 m m de diâmetro que está sujeito às forças concentradas. Os mancais de luva em A e B suportam somente forças verticais.
Determine o menor diâmetro admissível do eixo que está sujeita às forças concentradas. Os mancais de luva em A eB suportam somente forças verticais, e a tensão de flexão admissível é σ =160M P a .
Resolva o se o conjunto girar 45° e for assentado nos apoios.
A viga simplesmente apoiada é composta por quatro hastes de 16 mm de diâmetro, agrupadas como mostra a figura. Determine a tensão de flexão máxima na viga devido à carga mostrada.
A viga tem a seção transversal retangular mostrada na figura. Se P = 1,5 kN, determine a tensão de flexão máxima na viga. Faça um rascunho da distribuição de tensão que age na seção transversal..