Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 11

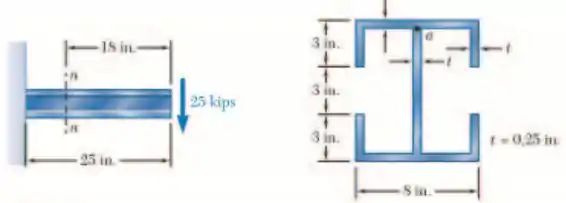
Para a viga e carregamento mostrado, considere a seção n-n e determinar (a) o maior tensão de cisalhamento nessa seção, (b) a tensão de cisalhamento ponto a.

Passo 1

E ai gurizada tudo beleza? O enunciado pede que a gente determinar (a) o maior tensão de cisalhamento nessa seção, (b) a tensão de cisalhamento ponto a..... Então partiu!

Começaremos esboçando o elemento para calcularmos a inércia :D

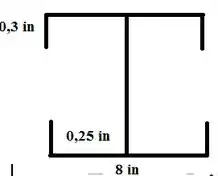
Calculando a inércia, temos:

I = 1 12 b h 3 - 1 12 b h 3 - 2 12 b h 3

Substituindo os valores temos:

I = 1 12 8 x 9 3 + 1 12 7,25   x   8,5 3 - 2 12 0 , 25   x   3 3 = 113,8   i n 4

Agora devemos determinar o momento como a imagem abaixo :D

M = 25 x 18 = 450   k i p   i n

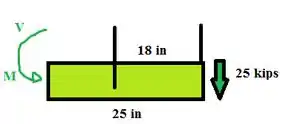
Passo 2

Maior tensão de cisalhamento nessa seção temos:

Q = 2 x 3 x 0,25 x 3 + 7,5 x 0,25 x 4,375 + 4,25 x 0,25 x 2,125 = 14,96   i n ³

Sendo a espessura de t= 0,25 in

Temos então:

t = V Q I t = 25 x 14,96 113,8   x   0,25 = 13,15   k s i

Passo 3

A tensão de cisalhamento ponto a

Q = 4,5   i n 3 + 8,2   i n 3 = 12,7   i n ³

Sendo a espessura de t= 0,1m

Temos então:

t = V Q I t = 25 x 1 2 , 7 113,8   x   0,25 = 1 1,6   k s i

Resposta

  1. 13,15   k s i
  2. 11,6   k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de aço ( E a = 200G P a ) e uma de alumínio ( E a l = 70G P a ) são firmemente unidas para formar a viga composta mostrada. Para uma força cortante vertical de 20k N , determinar (a) a tensã
Considerar a viga em balanço AB discutida na Sec 5.10 e a porção ACKJ da vga, que está localizada à esquerda da seção transversal CC’ e acima do plano horizontal JK onde K é um ponto a uma distancia y
Considerar a viga em balanço AB discutida na Sec 5.10 e a porção ACKJ da vga, que está localizada à esquerda da seção transversal CC’ e acima do plano horizontal JK onde K é um ponto a uma distancia y
Sabendo-se que o tubo estrutural mostrado tem uma espessura de parede uniforme 6 mm, determinar a tensão normal no ponto A e a tensão de cisalhamento no ponto B.
Sabendo-se que o tubo estrutural mostrado tem uma espessura de parede uniforme 6,3 mm, determinar a tensão normal no ponto A e a tensão de cisalhamento no ponto B.