Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 92
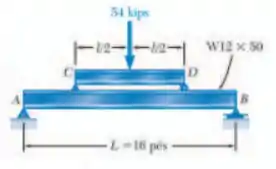
Uma carga de é para ser suportada pelo centro do vão da viga de . Sabendo que a tensão normal admissível para o aço utilizado é de , determine o menor comprimento da viga de modo que a viga da seção não fique sobrecarregado, o perfil de mesas largas mais econômico que pode ser empregado para a viga . Despreze o peso próprio de ambas as vigas.
Passo 1
Fala aí, pessoal. Beleza? Bora zerar esse livro.
Primeiro, vamos determinar o menor comprimento da viga de modo que a viga da seção não fique sobrecarregado. Para isso, vamos chamar de a distância entre os pontos e, que é igual à distância de à . Temos:
Pelas equações de equilíbrio, podemos utilizar as reações de equilíbrio no segmento :
Em seguida, já que temos o momento máximoe o enunciado nos forneceu a tensão normal admissível . Então, basta encontrarmos a outra variável da qual a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Para o perfil , . Subsituindo:
Opa, podemos igualar àquela relação que achamos anteriormente:
Agora que achamos o valor de , podemos substituir na relação com o comprimento . Fica assim:
Passo 2
Agora que determinamos o perfil para as vigas de cima, vamos repetir o processo para determinarmos o perfil para as vigas mestras. Então, bora esboçar o DCL:
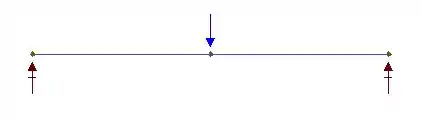
Em seguida, vamos calcular a reação de apoio através das equações de equilíbrio:
Por simetria, temos que , logo:
Assim, o momento fletor máximo vai ser no ponto médio da viga. E ele vai ser dado por:
Passo 3
Temos o momento máximoe o enunciado nos forneceu a tensão normal admissível , basta encontrarmos a outra variável da qual a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Subsituindo:
Então, vamos até o ábaco para encontrar o valor mínimo admissível do módulo de resistência imediamente maior que que encontramos. Portanto, o perfil escolhido é:
Que possui .
É isso, galera! Bora fazer mais exercícios pra ficar craque.