Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 57b

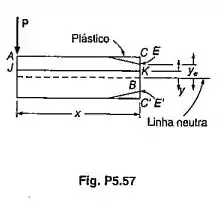
Considerar a viga em balanço AB discutida na Sec 5.10 e a porção ACKJ da vga, que está localizada à esquerda da seção transversal CC’ e acima do plano horizontal JK onde K é um ponto a uma distancia y < y c acima da linha neutra (veja a figura). Pede-se (a) Lembrando que σ x = σ e entre C e E e σ x = σ e / y e y entre E e K, mostrar que a intensidade da força cisalhante horizontal H exercida na face inferior da porça da viga ACKJ é

H = b σ e c - 1 2 y e - 1 2 ⋅ y 2 y e

(b) Observando que a tensão de cisalhamento em K é:

τ x y = lim Δ A → 0 ⁡ Δ H Δ A = lim Δ A → 0 ⁡ 1 b ⋅ Δ H Δ x = 1 b ⋅ ∂ H ∂ x

E lembrando que y e é uma função de x definida pela Eq. 5.18, desenvolver também a equação 5.19

Passo 1

Beleza, vamos dar uma olhada na equação:

τ x y = 1 b ⋅ ∂ H ∂ x

A gente tem uma equação para H . Vamos aplicar:

τ x y = 1 b ⋅ ∂ ∂ x b σ e c - 1 2 y e - 1 2 ⋅ y 2 y e

E efetuar a derivação:

τ x y = 1 b ⋅ b σ e ⋅ ∂ ∂ x c - 1 2 ∂ ∂ x y e - 1 2 ⋅ ∂ ∂ x y 2 y e

Como é dito no enunciado da questão, y e é uma função de x , então:

τ x y = - 1 2 σ e ⋅ ∂ ∂ x y e + y 2 ⋅ ∂ ∂ x y e - 1

τ x y = - 1 2 σ e ⋅ ∂ y e ∂ x + y 2 ⋅ ( - 1 ) y e - 2 ⋅ ∂ y e ∂ x

Chegamos em:

τ x y = - 1 2 σ e ⋅ 1 - y 2 y e ∂ y e ∂ x

Passo 2

O momento que atua sobre a seção é:

M = P ⋅ x

Seguindo a dica da questão, vamos dar uma olhada na equação 5.18 do livro:

P x = 3 2 M e 1 - 1 3 ⋅ y e 2 c 2

Vamos derivar por x :

∂ ∂ x P x = ∂ ∂ x 3 2 M e 1 - 1 3 ⋅ y e 2 c 2

P = 3 2 M e ∂ ∂ x 1 - 1 3 ⋅ y e 2 c 2

P = 3 2 M e - 1 3 ⋅ ∂ ∂ x y e 2 c 2

P = - 1 2 M e ⋅ ∂ ∂ x y e 2 c 2

P = - M e ⋅ y e c 2 ⋅ ∂ y e ∂ x

Logo:

∂ y e ∂ x = - P ⋅ c 2 M e ⋅ y e

Passo 3

∂ y e ∂ x = - P ⋅ c 2 M e ⋅ y e

Pra prosseguirmos, vamos ter que voltar na seção 4.10 . Como essa é uma seção retangular, podemos usar a equação 4.44 :

M e = 2 3 b c 2 σ e

Logo:

∂ y e ∂ x = - P ⋅ c 2 2 3 b c 2 σ e ⋅ y e

∂ y e ∂ x = - 3 P 2 σ e b y e

Passo 4

Agora é só a gente combinar o resultado do Passo 1 e do Passo 3:

τ x y = - 1 2 σ e ⋅ 1 - y 2 y e ∂ y e ∂ x

∂ y e ∂ x = - 3 P 2 σ e b y e

Logo:

τ x y = - 1 2 σ e ⋅ 1 - y 2 y e - 3 P 2 σ e b y e

E chegamos na equação que queremos demonstrar:

τ x y = 3 4 P b y e ⋅ 1 - y 2 y e

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b . 5.14 , considerando que a carga vertical de 120k N é removida.
Três forças são aplicadas a uma viga constituída de um perfil laminado W 150x29,8 , como mostrado. Determinar as tensões, normal e de cisalhamento, nos três pontos indicados.
Para uma viga extrudada de seção transversal mostrada, determinar:A distribuição das tensões de cisalhamento, causadas por uma força vertical V de 2,5k N aplicada em O .
Para uma viga extrudada de seção transversal mostrada, determinar:A localização do centro de cisalhamento O A distribuição das tensões de cisalhamento, causadas por uma força vertical V de 2,5k N apli
Para uma viga extrudada, com a seção transversal mostrada, determinar:A distribuição de tensões de cisalhamento, causando pela força cortante vertical V, aplicada em O.