Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 122
Resolva o considerando que as deformações medidas são:
Passo 1
Para essa questão temos dois itens a serem resolvidos, primeiro determinar a força que causa essas deformações nos pontos A e B e o respectivo braço de alavanca que causaria essas deformações.
Para isso temos que saber o seguinte, se temos deformações, temos como calcular tensões pela seguinte fórmula:
Mas pensa no seguinte, se queremos determinar as cargas que agem na seção, e temos as tensões, podemos pensar da seguinte forma.
- As tensões vão ser causadas pela carga axial que age na nossa seção, ou seja, a carga P espalhada pela área da seção,
- E como essa carga P tem um braço de alavanca, ela também vai causar um momento fletor, que também vai contribuir na nossa tensão.
Sendo assim, também podemos escrever as nossas tensões pela seguinte equação.
Tendo essas duas relações, precisamos agora começar a determinar o que temos, sendo assim podemos anotar no próximo passo.
Passo 2
- Dados do enunciado
- Dados da seção
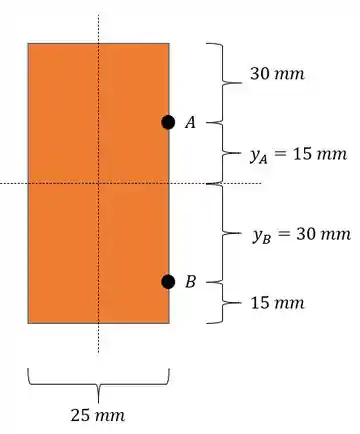
- Dados de Y para determinar o cálculo das tensões em A e B.
Pelos dados do enunciado temos que:
Sabemos que a nossa seção é dada com as seguintes dimensões.
A área da seção vai ser feita da seguinte maneira:
E o momento de inércia é calculado pela seguinte equação:
Sendo assim teremos que:
Calculando as tensões pela deformação, teremos que:
Analisando o outro grupo de fórmulas, temos que:
Subtraindo uma equação da outra teremos que:
Isolando o momento fletor, teremos que:
Mas do que adiante determinar o momento se queremos a carga aplicada? Ai basta usarmos o nosso sistema de equações de novo. Mas multiplicamos a primeira a equação por e a segunda por , sendo assim teremos que:
Subtraindo uma equação da outra, teremos que:
Como o objetivo é determinar a carga, teremos que:
E assim resolvemos o nosso item A, que pedia exatamente a carga que foi aplicada, e como o item B pede a distancia que foi aplicada, basta lembrarmos da seguinte fórmula:
O momento já determinamos, sendo assim teremos que: