Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 21

Para a viga e o carregamento mostrados, considere a seção n - n e determine a tensão de cisalhamento no (a) ponto a e (b) no ponto b

Passo 1

Muito bem gurizada, vamos começar? Vamos dividir a seção da viga em 2 vem comigo ;)

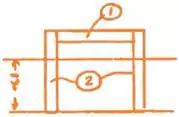
R A = R B =   25   k i p s na seção n-n V = 25   k i p s

Localizamos o centro e calculamos o momento de inércia.

Y _ = Σ A y _ Σ A = 72,94 15,75 = 4,631   i n .

I = Σ A y 2 + Σ I _ = 35,56 + 47,91 = 83,47   i n 3

Passo 2

Determinando a tensão de cisalhamento no ponto a

(A); Q a = A y _ = 3 4 1,5 4,631 - 0,75 = 4.366   i n 3

t = 3 4 = 0,75   i n τ a = V Q I t = 25 4,366 83,47 0,75

τ a = 1,74 4   k s i τ a = 12,3   M P a

Passo 3

Determinando a tensão de cisalhamento no ponto b

(B): Q a = A y _ = 3 4 3 4,631 - 1,5 = 7,045   i n 3

t = 0,75   i n . τ b = V Q I t = 25 7,045 83,47 0,75

τ b = 2,81   k s i τ b = 19,44   M P a

Resposta

(a) é: τ a = 12,3   M P a

(b τ b = 19,44   M P a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.
Determinar a tensão de cisalhamento no ponto a do bloco mostrado.
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.
Para a viga e o carregamento do Prob 5.92 , determinar: ( a ) o valor de β para que a tensão normal no ponto b seja zero; ( b ) a correspondente tensão normal no ponto a .
Sabendo-se que o tubo estrutural mostrado tem uma espessura da parede uniforme de 8m m , determinar a tensão de cisalhamento em cada um dos dois pontos indicados.