Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 60

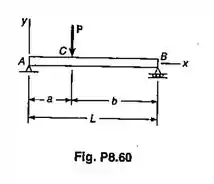
Para a viga com o carregamento mostrado, determinar: (a) a equação da linha elástica; (b) a declividade na extremidade A ;   (c) a deflexão no ponto C .

Passo 1

Fala aí galera. Bora estudar resmat. O primeiro passo para esta questão é determinar as reações de apoio .   Aplicando as equações de equilíbrio:

∑ M A = 0 → P a = a + b F B  

F B = P a a + b

∑ M B = 0 → P b = F A ( a + b )

F A = P b a + b

Portanto, a equação do momento em função de x pode ser calculada somando-se as parcelas do momento ao caminhar pela barra. Ela será:

M x = M x = F A x - P < x - a > 1

M x = P b a + b x - P < x - a > 1

A função - < x - a > 0 P é chamada de função degrau. Logo, ela só funciona quando temos x > a .   Quando x ≤ a ,   ela é nula.

Portanto, como a equação da linha elástica é dada por:

d y 2 d 2 x = M x E I

Teremos:

d y 2 d 2 x = P b a + b x - < x - a > 0 P E I

Passo 2

Agora, vamos integrar a equação acima uma vez em relação a x para acharmos declividade. Logo:

E I   θ = P b a + b x 2 2 - < x - a > 1 P + C 1

Para determinar C 1 ,   vamos usar as condições de contorno. Sabemos que θ 0 = - θ ( L ) ,   pois a declividade no primeiro apoio é igual ao inverso da declividade no segundo apoio. Ou seja:

E I   θ 0 = C 1

E I   θ L = P b a + b L 2 2 - < L - a > 1 P + C 1 = P b a + b L 2 2 - b P + C 1

C 1 = - P b a + b L 2 2 + b P - C 1

C 1 = - P b a + b L 2 4 + b P 2

Portanto:

E I   θ = P b a + b x 2 2 - < x - a > 1 P - P b a + b L 2 4 + b P 2

Iremos integrar a equação novamente em relação a x   para encontramos a deflexão. Ou seja:

E I   y = P b a + b x 3 6 - < x - a > 2 P 2   - P b a + b L 2 4 x + b P 2 x + C 2

Do mesmo modo, sabemos que:

y 0 = 0 → C 2 = 0

Pois no apoio não há deflexão.

Logo:

E I   y = P b a + b x 3 6 - < x - a > 2 P 2   - P b a + b L 2 4 x + b P 2 x

Passo 3

Agora, basta calcular os itens pedidos substituindo as posições nas fórmulas. Para a letra b:

E I   θ 0 = P b a + b 0 2 2 - < 0 > 1 P - P b a + b L 2 4 + b P 2

θ 0 = - P b a + b L 2 4 E I + b P 2 E I

Para a letra c:

E I y a = P b a + b a 3 6 - < a - a > 2 P 2   - P b a + b L 2 4 a + b P 2 a

y a = P b a + b a 3 6 E I   - P b a + b L 2 4 E I a + b P 2 E I a

Resposta

  1. d y 2 d 2 x = P b a + b x - < x - a > 0 P E I
  2. θ 0 = - P b a + b L 2 4 E I + b P 2 E I
  3. y a = P b a + b a 3 6 E I   - P b a + b L 2 4 E I a + b P 2 E I a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para os carregamentos mostrados, determinar:A equação da curva elástica para a viga AB;A deflexão da extremidade livre;A declividade da extremidade.
resolver as partes b e c do P r o b . 8.5 , considerando que a viga A B é um perfil laminado de aço W 310 x 52 e que W 0 = 40k N / m , L = 3,65 m e E = 200G P a .
A viga simplesmente apoiada A B é carregada com uma carga distribuída que varia linearmente como mostrado. Determinar:A equação da linha elástica;A deflexão no ponto médio do vão;A declividade na extr
A viga simplesmente apoiada A B é carregada com uma carga distribuída que varia linearmente como mostrado. Determinar:A equação da linha elástica;A deflexão no ponto médio do vão;A declividade na extr
Para a viga com o carregamento mostrado, determinar a deflexão no: a) ponto A b) ponto C.