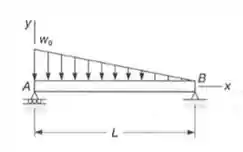
A viga simplesmente apoiada é carregada com uma carga distribuída que varia linearmente como mostrado. Determinar:
- A equação da linha elástica;
- A deflexão no ponto médio do vão;
- A declividade na extremidade ;
- Resolver as partes e , assumindo que a viga AB é um perfil laminado de aço e que , e .
Passo 1
Fala meu povo maravilhoso, estamos começando mais um capitulo e agora vamos resolver problemas que envolvem deslocamentos, ou como os professores gostam de chamar, deflexões, e por enquanto só vamos ver deflexões nas vigas. Para isso temos que saber o seguinte, a nossa equação, que determina as deflexões em uma viga, é dada por:
E ela pode parecer um monstro em uma primeira olhada, mas ela é muito simples e fácil de trabalhar.
- O que é o y?
- Y é a nossa deflexão, ou deslocamento, e se Integrarmos ele 4 vezes, teremos 4 incógnitas, mas em compensação, vamos ter a equação do deslocamento.
- Se integrarmos ele 3 vezes, teremos não mais a equação do deslocamento, mas da inclinação
- Se integrarmos 2 vezes teremos os momentos fletores.
- Se integrarmos uma, teremos o cortante.
- O que é o x?
- O que é o ?
- Carregamento concentrado
- Carregamento distribuído
- Carregamento triangular
- condições de contornos essenciais:
- condições de contornos naturais:
O x é bem simples, ele é o que define os pontos da nossa viga, ou seja, ele varia entre 0 e L, no nosso exemplo ele vai do ponto A até o ponto B.
Esse é a equação do carregamento, e ela é bem tranquila de representar.

Se tivermos cargas concentradas, seja de momento ou de força o nosso carregamento na equação será zero:

Se o carregamento for distribuído, então basta usarmos ele diretamente na equação, ou seja, basta fazermos:
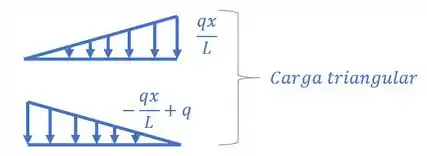
Se a carga for triangular, aí vai depender da posição, sendo assim podemos ter os dois casos acima:
E por fim a ultima coisa que precisamos saber são as condições de contorno, que são o que vai definir as incógnitas da nossa equação. As condições de contorno vão ser dadas por dois grupos:
essas condições são ligadas a deslocamentos e rotações, e olhando cada apoio vamos ter que:
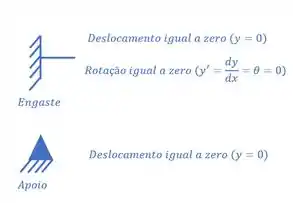
essas condições são ligadas a momentos e cortantes e variam de caso para caso, e são condições que podem ser determinadas diretamente na estrutura, por exemplo, apoios de primeiro e segundo gênero não impedem rotações, ou seja, sem precisar fazer nenhuma conta, já sabemos de antemão que nos apoios o momento vai ser igual a zero, mas podemos ver alguns outros exemplos aqui embaixo:

Agora que já sabemos o que os temos da nossa fórmula significam, vamos resolver ela, você vai ver que é algo muito tranquilo de ser feito, e vai sair daqui satisfeito em saber que é muito de boas, vamos nessa?
Passo 2
Vamos, lá, no nosso problema, a estrutura dada é:
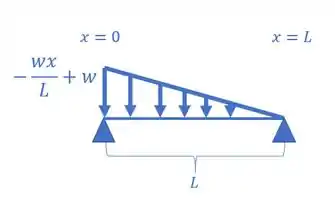
Como a nossa carga é distribuída, independente que essa carga seja no meio, ou no final ou no começo, teremos que:
Substituindo na nossa equação, teremos que:
Se integramos a primeira vez, vamos obter a primeira constante do nosso problema:
E vale lembrar que como já definimos, a primeira integral é o cortante, assim temos que:
Se integrarmos novamente, teremos a nossa segunda incógnita:
E sabemos que esse é o nosso momento fletor:
Se integramos novamente, teremos a nossa terceira incógnita:
E essa é a equação da rotação da nossa viga:
E por fim, a ultima integral vai dar o deslocamento e a nossa quarta incógnita:
Tendo a equação, basta olharmos as condições de contorno, e com elas podemos determinar a solução do nosso problema, vamos nessa? Já está acabando.
Passo 3
Para as condições, iremos olhar os extremos da viga, e é importante ver o seguinte, sempre a soma das condições de contorno deve ser igual ao número de incógnitas, ou seja, se temos 4 incógnitas, temos que ter 4 condições, podendo ser qualquer combinação de essenciais com naturais ( 1 natural e 3 essenciais, ou duas essenciais e duas naturais, ou 4 essenciais) não importa, no fim o total tem que ser 4, sendo assim teremos que:
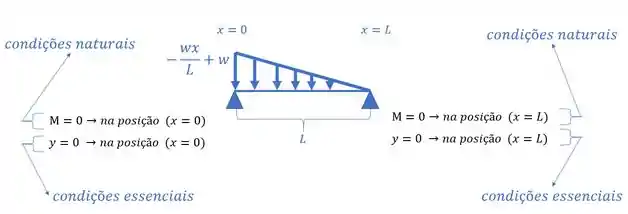
Ou seja, temos 4 condições, e com isso podemos resolver o nosso problema, sempre começando do menor número de incógnitas para o maior, sendo assim vamos ter que:
E assim determinamos todas as incógnitas do nosso problema, sendo assim basta substituirmos na nossa equação final.
E assim resolvemos o nosso item a)
Passo 2
O item b) quer saber o deslocamento no centro da viga, ou seja, queremos saber o deslocamento em , assim temos que:
No item c) queremos saber a rotação, para isso sabemos que a equação é dada por:
E queremos saber a rotação no ponto A, ou seja, no ponto .
Usando
Passo 3
Agora nosso objetivo é determinar os valores numéricos de deformação e declividade do ponto A, já sabemos que as equações são dadas por.
Já sabemos pelo enunciado que:
E sabemos que o comprimento da nossa barra é dada por:
E vale lembrar que a a carga distribuída também é dada por:
E o momento de inércia podemos obter pela seguinte tabela (lembrando que vamos considerar o nosso eixo em pé, ou seja, queremos o momento de inércia em torno de x na nossa tabelinha aqui de baixo.
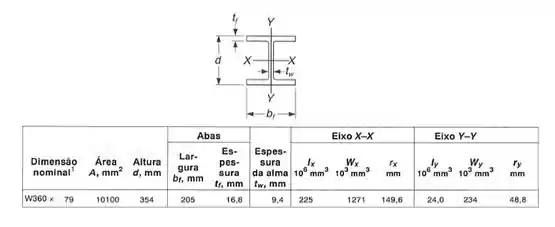
Substituindo primeiro a deformação, tem-se que: