Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 3
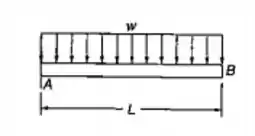
Para a viga uniforme em balanço, com o carregamento mostrado, determinar: a declividade da extremidade livre; a deflexão da extremidade livre.
Passo 1
E aí, gurizada do Respodeaí, beleza? Bora pra mais um exercício de Resmat para tirar aquele notão na prova.
Neste problema temos uma viga com uma das extremidades livre e outra engastada. Para encontrarmos a declividade no ponto , vamos utilizar o apêndice do nosso livro, a tabela de deformações de vigas, e nela encontrarmos a equação de rotação adequada para este caso, que corresponde ao caso da tabela. Logo:
E essa é a nossa a declividade na extremidade livre. Bora pra deflexão!
Passo 2
O próximo passo é a deflexão na extremidade livre, para a encontrarmos, temos que utilizar a tabelinha do apêndice de novo, só que dessa vez vamos procurar a equação da linha elástica. Ela é dada por:
Subsituindo:
Isso é tudo, pessoal.