Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 189

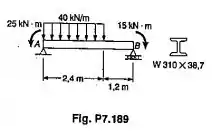
Para a viga com o carregamento mostrado, determinar: (a) a maior tensão normal devido à flexão; (b) a maior tensão de cisalhamento sobre uma seção transversal.

Passo 1

Fala aí galera do Responde aí. Partiu jantar a prova de resmat?

Essa questão nos pede a maior tensão normal e a maior tensão cisalhante. O primeiro passo é calcular as reações de apoio. Depois, devemos fazer os diagramas para pegar o maior esforço correspondente à tensão. Vamos lá:

∑ M A = 0 → 3,6 F B + 25 = 15 + 40 × 2,4 × 1,2

F B = 29,22   k N

∑ F y = 0 → F A + F B = 40 × 2,4

F A = 96 - 29,22 = 66,78   k N

Agora, vamos fazer os diagramas de cortante e momento fletor:

Cortante:

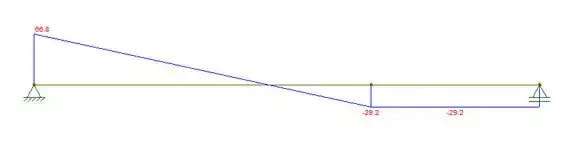
Momento:

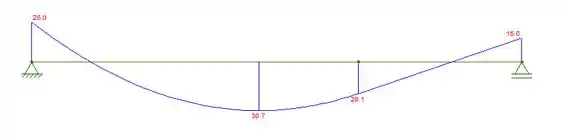
Passo 2

Agora, basta substituir nas fórmulas das tensões com os esforços máximos do diagrama.

Devemos consultar uma tabela com os valores do momento de inércia e as medidas para a seção.

As tensões são dadas por:

τ = V Q I t

σ = M y I

Logo:

V m a x = 66800   N

Q m a x = 24,85 × 77,5 = 1925,87   m m ³

I = 8581 0000   m m 4  

t = 5,8   m m

τ m á x = 66800 × 1925,87 5,8 × 85910000 = 0,258   M P a

Já para a tensão normal:

M m á x = 30,7   k N m

y = 155   m m

I = 85810000   m m 4  

σ m á x = 30,7 × 10 6 × 155 85810000 = 55,45   M P a

Resposta

τ m á x = 0,258   M P a

σ m á x = 55,45   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar: a) máximo tensão normal devido a flexão b) maior tensão de cisalhamento numa seção transversal devido à flexão.
Resolver o problema 7.32 considerando que P= 350 N e Q= 530 N
Determinar a) a distancia “a” para que o máximo valor absoluto do momento fletor na viga seja tão pequeno quanto possível B) a correspondente tensão normal, devido a flexão.
Sabendo-se que P=Q=530 N, determinar a) a distância para a, para que o máximo valor absoluto do momento fletor na viga seja tão pequeno quanto possível b) a correspondente tensão normal devido à flexã
Usando o método da sec 7.4 resolver o problema 7.3