Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 180

Para a viga com carregamento mostrado, projetar a seção transversal da viga, sabendo que a qualidade da madeira usada tem σ = 12,5 M P a   e τ = 930 k P a .

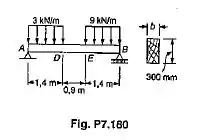
Passo 1

Fala aí galera, bora pra mais essa questão de resmat.

Primeiramente, temos que calcular as tensões e igualar à tensão admissível fornecida.

Primeiramente, devemos calcular as reações de apoio. Sabemos que:

∑ F y = 0 → F A + F B = 3 × 1,4 + 9 × 1,4 = 16,8

∑ M A = 0 → 0,7 × 3 × 1,4 + 9 × 1,4 × 2,9 = 3,7 F B

F B = 10,67 k N

F A = 16,8 - 10,67 = 6,13 k N

Passo 2

Sabemos que o maior momento atua no fim da carga distribuída de 9   k N / m , portanto, lá está a maior tensão normal. Já o maior cortante fica no apoio B   e lá se encontra a maior tensão cisalhante. Pegando o ponto de maior momento:

M = 1,4 × 10,67 - 9 × 1,4 × 0,7 = 6,118 k N / m

A fórmula da tensão normal é:

σ = M y I

Onde M   é o momento na seção, y   é a distância da linha neutra e I   é o momento de inércia da seção. Determinando o centroide e o momento de inércia da seção:

y - = 150

I = b × 300 3 12 = 2250000 b

Portanto, substituindo os valores na fórmula e isolando b :

σ = M y I

12,5 = 6118000 × 150 2250000 b

b = 32,62 m m

Passo 3

Agora, vamos fazer o mesmo para a tensão cisalhante. Ela é dada por:

τ = V Q I t

Onde V   é o cortante na seção, Q   é o momento estático, I   é o momento de inércia e t   é a espessura da seção, ou seja, t = b .  

O momento estático será:

Q = A y - = 150 × b × 75 = 11250 b

Logo, substituindo e isolando b (lembrando que usaremos a seção com maior cortante, que fica no apoio B):

τ = V Q I t

0,93 = 10,67 × 1000 × 11250 b 2250000 b 2

b = 57,36 m m

Passo 4

Agira, devemos escolher o melhor valor de b   para a situação. Note que nas duas fórmulas o momento de inércia é inversamente proporcional à tensão. Logo, devemos optar pelo maior momento de inércia e, consequentemente, um maior b .   Portanto:

b = 57,36 m m

Resposta

b = 57,36 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrado, determinar: a) máxima tensão normal numa seção transversal em D; b) a máxima tensão de cisalhamento numa transversal imediatamente à direita de A. Assumir que τ=
Para a viga e o carregamento mostrado, determinar: a) máxima tensão normal numa seção transversal em D; b) a máxima tensão de cisalhamento numa transversal imediatamente à direita de A. Assumir que τ=
Para a viga e o carregamento mostrado, determinar: a) máxima tensão normal numa seção transversal em C; b) a máxima tensão de cisalhamento numa transversal imediatamente à esquerda de B.
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar a máxima tensão normal devido à flexão.
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar o máximo valor absoluto a) força cortante b) momento fletor.