Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 18

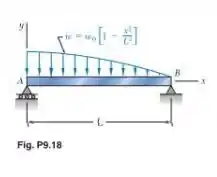
Para a viga e o carregamento mostrados, determine (a) a equação da linha elástica, (b) a inclinação na extremidade A   e (c) a deflexão no ponto médio do vão.

Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Neste tipo de questão, vamos utilizar a equação da linha neutra para acharmos a deflexão pedida.

Sabemos que a equação da linha neutra é dada por:

E I d 2 y d x 2 = M x

Logo, precisamos da equação do momento. Além disso, integrando a equação uma vez, temos a equação da rotação e, integrando duas vezes, temos a equação da deflexão. Todas as equações citadas acima são em função da distância x   axial à estrutura, indo da esquerda para a direita.

Para determinar a equação do momento, usaremos algumas equações auxiliares. Sabemos que:

d V d x = - w  

Como w   é fornecido, teremos:

d V d x = w 0 L 2 x 2 - L 2  

Portanto, integrando os dois lados em função de x :

V = w 0 L 2 x 3 3 - L ² x + C 1

Também sabemos que:

d M d x = V = w 0 L 2 x 3 3 - L ² x + C 1

Logo, integrando novamente:

M = w 0 L 2 1 12 x 4 - 1 2 L ² x ² + C 1 x + C 2

Aplicando as condições de contorno:

x = 0 → M = 0

C 2 = 0

x = L → M = 0

C 1 = 5 12 w 0 L

Portanto, a equação do momento é:

M = w 0 L 2 1 12 x 4 - 1 2 L ² x ² + 5 12 w 0 L x

Passo 2

Agora, com a equação do momento encontrada, basta substituir na equação da linha neutra e integrar duas vezes. Logo:

E I d 2 y d x 2 = w 0 L 2 1 12 x 4 - 1 2 L ² x ² + 5 12 w 0 L x

Colocando em evidência:

E I d 2 y d x 2 = w 0 L 2 1 12 x 4 - 1 2 L 2 x 2 + 5 12 L ³ x

Logo, integrando-se duas vezes para acharmos a equação da linha elástica.

E I d y d x = w 0 L 2 1 60 x 5 - 1 6 L 2 x 3 + 5 24 L ³ x ² + C 1

E I   y = w 0 L 2 1 36 0 x 6 - 1 24 L 2 x 4 + 5 72 L 3 x 3 + C 1 x + C 2

Passo 3

Para determinar as constantes de integração, vamos aplicar algumas condições de contorno. Sabemos que, nos dois apoios, a deflexão será nula:

x = 0 → y = 0

X = L → y = 0

Logo:

C 2 = 0

C 1 = - 11 360 w 0 L ³

Passo 4

Pronto, já temos todas as incógnitas. Basta listar o que o problema pede. Na letra a ,   a equação da linha elástica será:

y = w 0 x 6 - 15 L 2 x 4 + 25 L 3 x 3 - 11 L 5 x 360 E I L 2

Passo 5

Para a letra b, basta substituir a posição do ponto A na equação da rotação. Logo:

x = 0

d y d x = - 11 360 w 0 L 3 E I

Substituindo os valores:

θ A = - 11 360 w 0 L 3 E I

Passo 6

Para a letra c ,   basta substituir x = L 2 na equação da linha elástica. Logo:

y c = - 211 23,04 w 0 L 4 E I    

Resposta

  1. y = w 0 x 6 - 15 L 2 x 4 + 25 L 3 x 3 - 11 L 5 x 360 E I L 2
  2. θ A = - 11 360 w 0 L 3 E I
  3. y c = - 211 23,04 w 0 L 4 E I    
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga de madeira e o carregamento mostrados na figura, determine (a) a inclinação na extremidade A e (b) a deflexão no ponto médio C. Use E = 12 GPa.
Para a viga de madeira e o carregamento mostrados na figura, determine (a) a inclinação na extremidade A e (b) a deflexão no ponto médio C. Use E = 29.10 6 psi.
Para a viga de madeira e o carregamento mostrados na figura, determine (a) a reação no apoio móvel (b) a deflexão no ponto C.
Para a viga de madeira e o carregamento mostrados na figura, determine (a) a reação no apoio móvel (b) a deflexão no ponto C.
Para a viga de madeira e o carregamento mostrados na figura, determine (a) a inclinação na extremidade A e (b) a deflexão no ponto médio C. Use E = 200 GPa.