Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 17
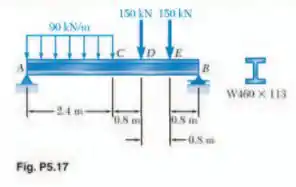
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Vamos para mais uma questão.
Como queremos a tensão normal máxima gerada pelo momento fletor na seção , devemos, primeiramente, determinar o valor do momento fletor na seção Para isso, precisamos determinar as reações e encontrar o diagrama. O DCL é dado por:
Para acharmos as reações, vamos utilizar as equações de equilíbrio. Sabemos que:
Também sabemos que:
Portanto, podemos esboçar o diagrama de momento. Fazendo ele:
Podemos ver que o momento em equivale a
Passo 2
Já temos o momento na seção basta encontrar as outras variáveis das quais a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é a distância da linha neutra (onde a tensão é nula) até o ponto em que queremos saber a tensão e é o momento de inércia da seção.
Esses valores são tabelados para o perfil indicado, que é o W 460X113 Os valores podem ser encontrados em tabelas na internet ou no próprio livro.
Como queremos a máxima tensão, pegaremos o maior Portanto, usando o ábaco:
O momento de inércia também está no ábaco, e é igual a:
Passo 3
Agora, temos todos os dados para obter a tensão normal na seção Substituindo os valores:
E pronto! Esta é a tensão normal na seção gerada pelo momento fletor.