Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 100

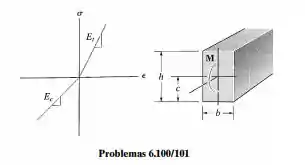
A viga é feita de um material com módulo de elasticidade sob compressão diferente do módulo de elasticidade sob tração. Determine a localização c do eixo neutro e deduza uma expressão para a tensão de tração máxima na viga cujas dimensões são mostradas na figura se ela estiver sujeita ao momento fletor M .

Passo 1

Não desanime! Tudo vai dar certo!

Como podemos observar, na região acima de c ocorrerá a tensão e força de compressão e abaixo ocorrerá a tensão e força tração. Na linha c , não existem forças ou deformações.

Dados fornecidos:

M

h

b

c

E c

E t

Passo 2

Agora trabalharemos para descobrir os valores das tensões σ m á x .

Utilizando a lei de Hooke podemos definir:

σ = E ϵ

Como temos duas tensões diferentes:

σ ( m á x ) c = E c ϵ ( m á x ) c

σ ( m á x ) t = E t ϵ ( m á x ) t

Podemos ainda correlacionar ϵ m á x t com ϵ m á x c através de uma semelhança de triângulos.

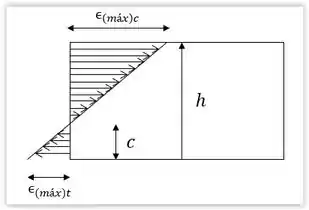
Sendo assim:

ϵ m á x t c = ϵ m á x c h - c

ϵ m á x c = ϵ m á x t ⋅ h - c c

Com a contração máxima ( ϵ m á x ( c ) ) podemos calcular a tensão máxima de compressão:

σ m á x ( c ) = E c ⋅ ϵ m á x c =   E c ⋅ ϵ m á x t ⋅ h - c c

Agora temos de fazer o somatório das forças para encontrar outras relações entre as tensões. Como o corpo está em repouso a força resultante é zero.

∑ F = 0

F t = F ( c )

σ m á x c ⋅ A c = σ m á x t ⋅ A t

σ m á x c ⋅ 1 2 ⋅ b ⋅ h - c = σ m á x t ⋅ b ⋅ c

σ m á x c ⋅ h - c = σ m á x t ⋅ c

σ m á x ( c ) = c h - c ⋅ σ m á x t

Agora se substituirmos os valores das tensões teremos:

  E c ⋅ ϵ m á x t ⋅ h - c c ⋅ h - c = E t ⋅ ϵ m á x ( c ) ⋅ c

E c ⋅ ϵ m á x t ⋅ h - c c ⋅ h - c = E t ⋅ ϵ m á x c ⋅ c

E c ⋅ h - c 2 = E t ⋅ c 2

E t E c = c h - c

Isolando c para encontrar a linha neutra.

c = h E c E t 1 + E c E t

c = h ⋅ E c E t + E c

Passo 3

Agora realizaremos a somatória dos momentos para encontrar a tensão de tração máxima. Como o corpo se encontra em equilíbrio o momento total é zero.

∑ M = 0

M = F t ⋅ d t + F c ⋅ d c

M = F t ⋅ 2 3 c + F c ⋅ 2 3 ( h - c )

M = 1 2 ⋅ c ⋅ σ m á x t ⋅ b ⋅ 2 3 c + 1 2 ⋅ h - c ⋅ σ m á x c ⋅ b ⋅ 2 3 ( h - c )

M = 1 3 c 2 ⋅ b ⋅ σ m á x t + 1 3 h - c 2 ⋅ b ⋅ σ m á x ( c )

Utilizando a equação anterior que relaciona a tenção de compressão máxima com a tensão de tração máxima:

M = 1 3 c 2 ⋅ b ⋅ σ m á x t + 1 3 h - c 2 ⋅ b ⋅ c h - c ⋅ σ m á x t

M = 1 3 c ⋅ b ⋅ σ m á x t ⋅ ( h - c + c )

Isolando a σ m á x t :

σ m á x t = 3 ⋅ M b ⋅ h ⋅ c

Substituindo o valor de c :

σ m á x t = 3 ⋅ M b ⋅ h 2 ⋅ E t + E c E c

Resposta

σ m á x t = 3 ⋅ M b ⋅ h 2 ⋅ E t + E c E c

c = h ⋅ E c E t + E c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrados, determine as equações das curvas de força cortante e momento fletor e o valor absoluto do momento fletor máximo na viga, sabendo que ( a ) k = 1 , bk = 0,5 .
Determine ( a ) a distância a para a qual o valor absoluto do momento fletor na viga seja o menor possível, ( b ) a correspondente tensão normal máxima em razão da flexão.
Desenhe os diagramas de força cortante e momento fletor para a viga e o carregamento mostrados e determine e determine a tensão máxima em razão do momento.
Desenhe os diagramas de força cortante e momento fletor para a viga e o carregamento mostrados e determine e determine a tensão máxima em razão da flexão.
Sabendo que o momento mostrado atua em um plano vertical, determine a tensão no:Ponto APonto B