Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 8

Determine as equações da linha elástica para a viga utilizando as coordenadas x 1 e x 3 . Especifique a inclinação em A e o deslocamento no centro do eixo. EI é constante.

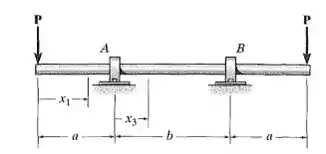
Passo 1

Por simetria, sabemos que as reações valem P.

Logo, para 0 ≤ x 1 ≤ a :

M x 1 = - P x 1

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = - P x 1

E I d v 1 d x 1 = - P 2 x 1 2 +   C 1

E I v 1 = - P 6 x 1 3 + C 1 x 1 + C 2

Para a ≤ x 3 ≤ b :

M x 3 = - P x 3

Logo:

E I d 2 v 3 d x 3 2 = - P a

E I d v 3 d x 3 = - P a x 3 ² + C 3

E I v 2 = - P a 2 x 3 3 + C 3 x 3 + C 4

Passo 2

As condições de contorno serão:

x 1 = a → v 1 = 0

x 3 = 0 → v 3 = 0

  x 3 = b 2 → d v 3 d x 3 = 0

x 1 = a   e x 3 = 0 → d v 1 d x 1 = d v 3 d x 3

Logo, substituindo:

C 1 = P a 2 a + b ; C 2 = - P a 2 6 ( 2 a + 3 b ) ; C 3 = P a b 2 ; C 4 = 0

Passo 3

As equações ficam:

v 1 = P 6 E I - x 1 3 + 3 a a + b x 1 - a ² ( 2 a + 3 b )

v 3 = P a 6 E I x 3 ( - x 3 + b )

Passo 4

A inclinação máxima ocorre em x 1 = a , e será dada por:

θ a = P a b 2 E I

O deslocamento no centro será dado por:

v c = P a b 2 8 E I

Resposta

v 1 = P 6 E I - x 1 3 + 3 a a + b x 1 - a ² ( 2 a + 3 b )

v 3 = P a 6 E I x 3 ( - x 3 + b )

θ a = P a b 2 E I

v c = P a b 2 8 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

( a ) Usando funções de singularidade, escreva as equações definindo a força cortante e o momento fletor para a viga e o carregamento mostrados. ( b ) Use a equação obtida para M para determinar o mom
Duas placas de reforço, cada uma com 15,88m m de espessura, são soldadas a uma viga W 760 × 147 . Conforme mostra a figura. Sabendo que σ a d m = 151,7M P a para a viga e as placas, determine o valor
Duas placas de reforço, cada uma com 15,88m m de espessura, são soldadas a uma viga W 760 × 147 . Conforme mostra a figura. Sabendo que l = 2743m m e b = 304,8m m , determine a tensão normal máxima em
Trace os diagramas de força cortante e momento fletor para a viga e o carregamento mostrados e determine e determine o valor máximo absoluto ( a ) da força cortante e ( b ) do momento fletor.
A viga A B , de comprimento L e seção transversaç quadrada de lado a , é apoiada por um pivô em C e carregada conforme mostra a figura. ( a ) Verifique se a viga está em equilíbrio. ( b ) Mostre que a