Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 68
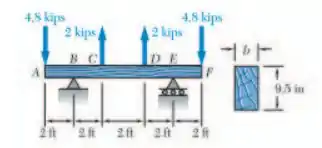
Para a viga e o carregamento mostrados na figura, projete a seção transversal da viga sabendo que o tipo da madeira utilizada tem uma tensão normal admissível de .
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.
Como queremos a a altura da seção transversal dada a tensão normal admissível, devemos, primeiramente, traçar o diagrama do momento fletor e, assim, identificar o seu ponto de máximoPara isso, precisamos determinar as reações e encontrar o diagrama. O DCL é dado por:
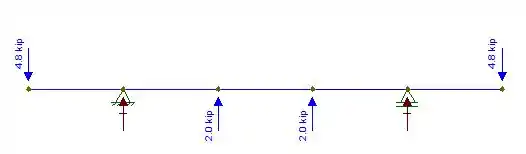
Para acharmos as reações, vamos utilizar as equações de equilíbrio. Sabemos que, por simetria:
Logo:
Portanto, podemos esboçar o diagrama de força cortante. Fazendo ele:
E também, o diagrama de momento:
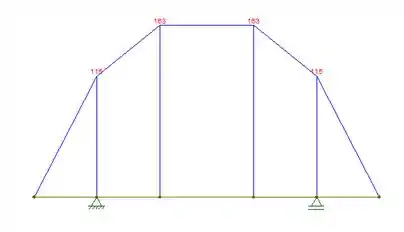
Com os diagramas traçados, podemos ver que o momento fletor máximo:
Agora, vamos determinar a distância da seção.
Passo 2
Já temos o momento máximoagora basta encontrar a outra variável da qual a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Subsituindo:
E então, para encontrarmos o comprimento da seção basta substituirmos os valores que temos na seguinte fórmula para o módulo de resistência para uma seção retangular. Temos: