Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 50
Resolva o Problema 7.28 usando o círculo de Mohr.
Passo 1
Beleza! Para esse exercício nós vamos utilizar a equação para o raio do círculo de Mohr para encontrar o valor de . Depois disso, para encontrar as tensões principais correspondentes, vamos utilizar a equação da tensão média, junto com o raio do círculo de Mohr.
Passo 2
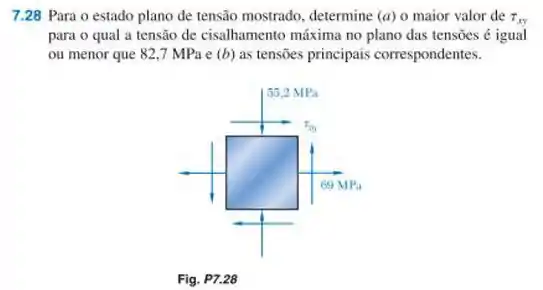
Então vamos lá! Vamos começar escrevendo as tensões que temos de acordo com o elemento dado no enunciado, então teremos:
Então, se o enunciado nos disse que a tensão de cisalhamento máxima no plano das tensões tem que ser igual ou menor que 82,7 MPa, vamos tomar o caso limite, em 82,7 MPa. Sabemos que, no estado plano de tensões, esse valor de cisalhamento corresponde ao raio do círculo de Mohr, então teremos:
Passo 3
Agora então, sabendo que a equação para o raio do círculo de Mohr é dada por:
Podemos isolar dessa equação, já que temos todos os outros valores e queremos justamente o valor de , então, fazendo isso, teremos:
Substituindo os valores conhecidos nessa equação, chegamos no valor da tensão de cisalhamento pedida na letra (a):
Opa, tá aí o que foi pedido na letra (a). Como estamos interessados no maior valor do cisalhamento, não precisamos nos preocupar com a orientação dele, só nos interessa o seu módulo.
Passo 4
Agora, para a letra (b), nós sabemos que as tensões principais podem ser dadas por:
Nós já temos o valor de R, que vimos lá no passo 2. Então precisamos calcular o valor da tensão média, que é dada por:
Substituindo os valores conhecidos, temos:
Então, as tensões principais serão:
Proonto! Finalizamos mais um!