Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 38
Usando o método da Seção , resolva o Problema .
Para a viga e carregamento mostrados, trace os diagramas de força cortante e momento fletor.
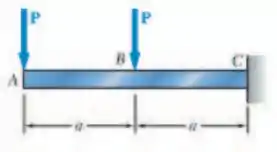
Passo 1
Fala galera, beleza? Vamos fazer mais questões pra ficar craque nessa matéria.
Para encontrarmos os diagramas de força cortante e momento fletor pedidos, precisamos esboçar o DCL do problema:
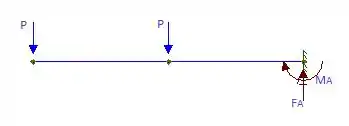
Com o esboço do DCL, podemos encontrar as reações de apoio através das equações de equilíbrio. Fica assim:
E também:
E assim, vamos determinar a força cortante para toda a viga.
Passo 2
Para isso, temos uma relação que nos diz que a inclinação de uma viga carregada, dada por , da curva da força cortante é negativa e a intensidade da inclinação em qualquer ponto é igual à força por unidade de comprimento naquele ponto:
Portanto, para o segmento :
E para o segmento , temos:
Opa, essa são as nossas equações para a força cortante. Podemos esboçar seu diagrama assim:
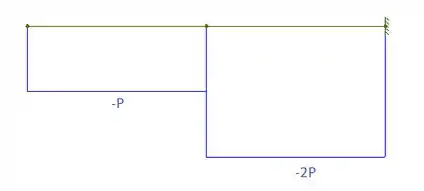
Agora que encontramos a equação e o diagrama para a força cortante, bora fazer o mesmo para o momento fletor.
Passo 3
Para determinarmos as equações para o momento fletor, devemos integrar a força cortante nos mesmos segmentos que usamos para a força cortante. Para :
E para o segmento , temos:
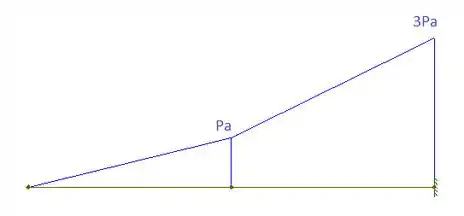
Assim, podemos escoçar o diagrama de momento cortante:
Isso é tudo, pessoal!!!
Resposta
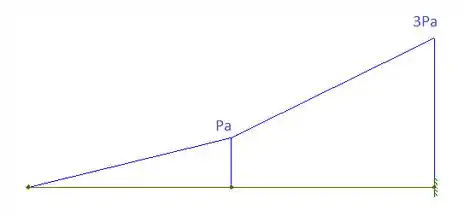
Cortante:
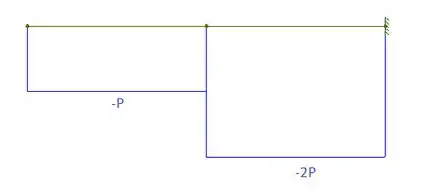
Momento:
