Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 85

Para a viga e o carregamento mostrados nas figuras, a deduza as equações das curvas de esforço cortante e momento fletor, b determine a intensidade e a localização do máximo momento fletor.

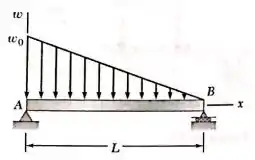
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiramente, vamos desenhar o diagrama de corpo livre considerando a carga distribuída:

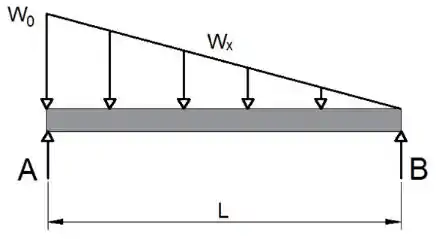
Sabemos que a carga triangular em qualquer ponto x da viga é calculada a partir da seguinte equação:

w x = w o 1 - x L

A carga concentrada devido a carga distribuída é igual a:

F R = w o ⋅ L 2

Portanto, temos o seguinte diagrama de corpo livre:

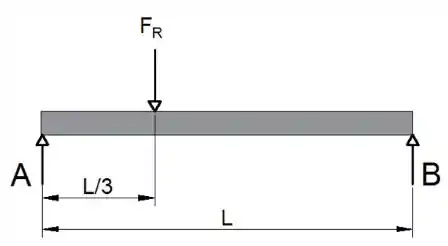
Passo 2

Vamos fazer o somatório dos momentos no ponto A :

↶ + ∑ M A = 0

L 3 w o ⋅ L 2 - L B y = 0

B y = w o ⋅ L 6

Fazendo agora o somatório das forças na horizontal, temos:

↑ + ∑ F y = 0

A y - w o ⋅ L 2 + w o ⋅ L 6 = 0

A y = w o ⋅ L 3

Passo 3

Sabemos que, a variação da força cortante é igual a integral da função da carga distribuída em função da distância.

Considerando um ponto C qualquer a uma distância x da reação de apoio A temos que a sua cortante neste ponto pode ser representada por:

V A - V C = ∫ 0 x w x d x

Para A :

V A = A y = w o ⋅ L 3

Substituindo os valores na equação, temos:

w o ⋅ L 3 - V x = ∫ 0 x w o 1 - x L d x

Resolvendo, temos:

V x = w o ⋅ L 3 - w o x - w o x 2 2 L 0 x

V x = w o ⋅ L 3 - w o x + w o x 2 2 L

V x = w o ⋅ L 3 - w o x L L + w o x 2 L 2 L 2

Reorganizando, temos:

V x = w o L 1 3 - x L + 1 2 x L 2

Passo 4

Para determinar o momento fletor máximo precisamos encontrar o ponot onde a cortante é igual a zero. Portanto para V = 0 , temos:

2 3 - 2 x L + x L 2 = 0

Resolvendo por bhaskara, encontramos:

x L = 1 - 1 3

Passo 5

Sabemos que o momento fletor é a integral da equação da força cortante, portanto:

d M d x = V

M = ∫ 0 x V x d x

Substituindo, temos que:

M = ∫ 0 x L V x L d x L

M x = w o L 2 1 3 x L - 1 2 x L 2 + 1 6 x L 3

Temos como momento máximo:

M m á x = 0,064 w o L 2

Resposta

a )   V x = w o L 1 3 - x L + 1 2 x L 2

M x = w o L 2 1 3 x L - 1 2 x L 2 + 1 6 x L 3

b )   M m á x = 0,064 w o L 2

x = 1 - 1 3 L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

74- Usando o método da Seção 7.6 , resolva o Problema 7.42
71- Usando o método da Seção 7.6 , resolva o Problema 7.39 .
72- Usando o método da Seção 7.6 , resolva o Problema 7.40
Para o carregamento na viga determine (a) os diagramas de momento fletor e cortante e (b) os valores absolutos máximos de momento fletor e esforço cortante.
Se a = 0,3 e a reação é uniformemente distribuída no solo, determine (a) os diagramas de cortante e momento fletor e (b) os valores máximos absolutos de momento e cortante.