Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 103
Sabendo que e , determine a intensidade da força necessária para se manter o equilíbrio.
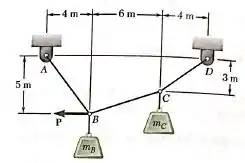
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro vamos calcular a força peso causada pelas massas. Temos que:
E:
Passo 2
Temos que o corpo livre do segmento é dado por:
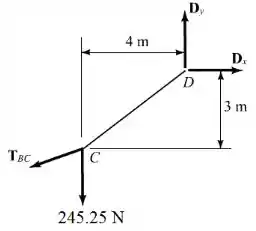
Analisando o somatório de momentos no ponto , temos:
Passo 3
Analisando agora o diagrama do segmento , temos:
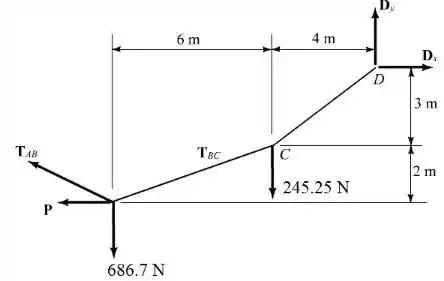
Como já temos a relação:
É só substituir na equação anterior:
Resolvendo, temos que:
Logo:
Passo 4
Finalmente, podemos analisar o diagrama do sistema inteiro:
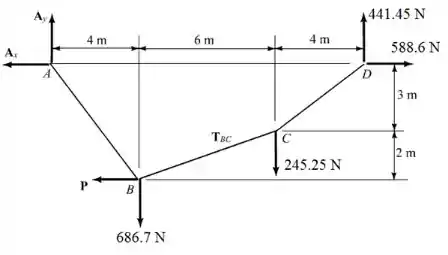
Tomando o momento sobre o ponto :
Resposta
Exercícios de Livros Relacionados
Para a viga mostrada A B , trace os diagramas de esforço cortante e de momento fletor e determine a intensidade e a localização do máximo valor absoluto do momento fletor, sabendo que (a) P = 27k N ,
Sabendo que a intensidade da carga concentrada P é 340N , (a) trace os diagramas de esforço cortante e o momento fletor para a viga A B , (b) determine o máximo valor absoluto do esforço cortante e mo
Resolva o problema 7.162 considerando que d C = 2,7m .
Uma tubulação de óleo é sustentada em intervalos de 1,8m , por ganchos verticais presos ao cabo mostrado na figura. Em razão do peso combinado do tudo e seu conteúdo, a tração em cada gancho é de 1800
29. Para a viga e o carregamento mostrados nas figuras, (a) trace os diagramas de esforço cortante e de momento fletor, (b) determine os valores absolutos máximos do esforço cortante e do momento flet