Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 1
Para a viga e carregamento mostrados, trace os diagramas de força cortante e momento fletor e determine as equações das curvas de força cortante e momento fletor.
Passo 1
Fala aí galera, beleza? Bora resolver mais um exercício.
Para encontrarmos os diagramas de força cortante e momento fletor pedidos, precisamos determinar as reações de apoio. Então, vamos esboçar o DCL do problema:
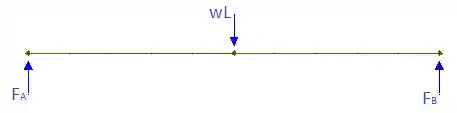
Para encontrarmos essas reações, vamos usar as equações de equilíbrio:
Como temos uma viga simétrica, temos que , logo:
Passo 2
Com isso, vamos esboçar um segundo DCL, agora do segmento . Temos:
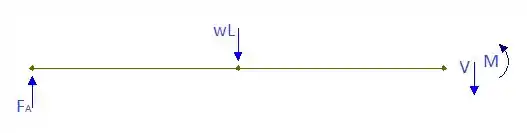
E assim, vamos utilizar as equações de equilíbrio para determinarmos as equações pedidas. Para a equação de força cortante, temos:
E para encontrarmos a equação do momento fletor, temos:
Opa, já encontramos as equações do momentos fletor e força cortante. Vamos esboçar os diagramas! Para a força cortante, temos:
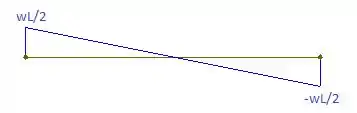
E para o momento cortante:
É isso, pessoal!!!
Resposta
Cortante:
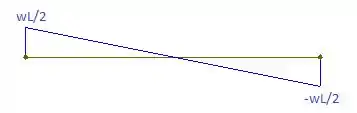
Momento:
