Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 54
Para a viga de concreto mostrada na figura, o modulo de elasticidade é de para o concreto e de para o aço. Sabendo que e e usando a tensão admissível de para o concreto e de para o aço, determine:
- A área necessária do reforço de aço considerando que a viga deve ser balanceada e.
- O maior momento fletor admissível. (veja o problema 4.53 a definição de viga balanceada.)
Passo 1
Fala galera, essa questão pode parecer que foge um pouco do padrão do que estávamos fazendo, mas não, ela ainda é bem tranquila de ser resolvida, porque ela vai suar conceitos bem parecidos com o que já estávamos vendo, só vamos ter alguns macetinhos novos pra ajudar a gente, com isso, bora meter a mão na massa.
Sabemos que o nosso fator a ser calculado é dado por:
Nesse tipo de questão, o macete vai ser sempre transformar o aço em concreto, assim, vamos ter que:
E o que fazíamos com esse fator? Multiplicávamos ele pela largura da nossa seção, certo? Aqui vamos usar um conceito parecido, porém, não igual, porque vamos ter que multiplicar pela área da seção de aço, e para isso precisamos saber o tamanho da nossa seção, e é bem simples, eu vou pegar a distância entre centros de barras, e com isso teremos a seguinte seção:
Temos que a área total das nossas barrinhas de aço são dadas por e a mudança que vamos fazer é exatamente na área de aço, assim vamos ter que:
E agora que fizemos isso, vamos aprender um macete MUITO MANEIRO, para determinarmos a LN, é tão maneiro que vou explicar ele no próximo passo.
Passo 2
Para determinarmos a LN eu vou primeiro mostrar a seção e depois explico ela, no caso, a nossa seção vai virar o seguinte:
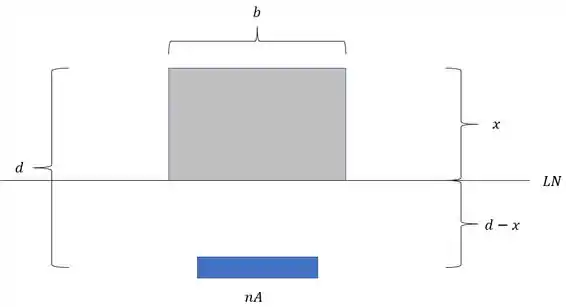
Agora perceba o seguinte, veja que a largura da seção de concreto e a distância do centroide da região que está o aço foram mantidos intactos, são exatamente iguais a primeira seção que fizemos, o que tem de novo?
- Primeiro, ao invés de usarmos a área da seção de aço normal, estamos usando a de aço modificada
- Segundo, perceba que eu posicionei a LN no que eu representei como o final da seção de concreto, isso significa que a seção de concreto realmente acaba ali? Não não, isso é só um macete para podermos fazer as contas.
Concreto é muito fraquinho para tração, então quem obrigatoriamente vai segurar a tração é o aço, por isso colocamos a REGIÃO toda do aço abaixo da LN.
Em contra partida, o concreto é muito TOP com compressão, e ele quem vai segurar a compressão toda, por isso fazemos ele totalmente acima da LN. Sacou a facilidade? Fazendo isso a gente consegue saber bem onde usar dados do aço e onde usar dados do concreto.
E a LN? Para acharmos ela, vamos ter que usar uma relação de tensões, com a tensão de concreto e a tensão do aço que o enunciado nos dá, assim sabemos que:
E veja que já sabemos o valor dos nossos y, assim temos que:
Assim temos que:
Dividindo uma tensão pela outra temos que:
E sabemos que:
Substituindo, teremos que:
E substituindo os valores, teremos que:
E sabemos também que podemos calcular a LN pela relação de área que temos, assim, voltando com o desenho, temos que:
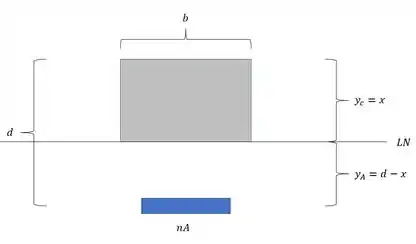
Multiplicando a área de concreto pelo centroide dele até a LN e igualando com a área de aço modificada multiplicada pelo centroide dela, teremos que:
E sabemos que:
E assim obtemos a nossa área de aço e resolvemos o item A) vamos para o item B)
Passo 3
Nosso objetivo é determinar o máximo momento, e a fórmula que relaciona a tensão com o momento é dado por:
E se verificarmos a estrutura que foi transformada, no caso o aço, teremos que usar a seguinte equação:
E para o momento de inércia temos que:
e para o aço teremos que:
Como a altura é muito, muito, muito pequena, podemos considerar a primeira parte zero, assim temos que:
Assim teremos que:
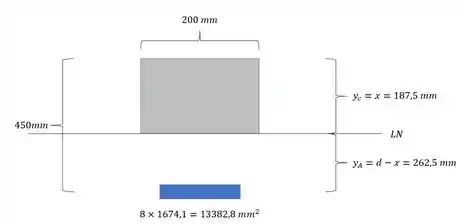
E sabemos que para os valores de y temos que:
- Verificando o concreto
- Verificando Aço
Assim temos que:
Assim temos que:
Como queremos o momento mais seguro, precisamos escolher o menor dos dois, assim o nosso momento vai ser dado por: