Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 119
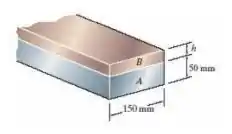
A viga composta é feita de alumínio 6061-T6 (A) e latão vermelho C83400 (B). Determine a dimensão h da tira de latão de modo que o eixo neutro da viga esteja localizado na costura dos dois metais. Qual é o momento máximo que essa viga suportará se a tensão de flexão admissível para o alumínio for (σadm)al = 128 MPa e para o latão (σadm )lat = 35 MPa?
Passo 1
Faaaala, galera boa, tudo bem? Bom bora resolver essa viga composta aqui! Pra fazer isso a gente vai ter que trabalhar com as fórmulas das seções equivalentes, e vai funcionar como se fosse de um material só pois a gente vai converter todas as dimensões de um dos dois materiais.
A primeira coisa que precisamos achar é a relação entre os coeficientes Eal e Elat. Para que possamos converter as dimensões do alumínio e aplicar o método da seção
n = =
Assim a nova base do alumínio será:
Passo 2
Agora se liga, já que a gente encontrou a nova base do alumínio, como se fosse de latão a gente pode fazer o cálculo da posição da linha neutra e isolar o h, a gente sabe que a posição é 50mm, assim:
Resolvendo essa equação temos:
Passo 3
Agora que já temos nosso h, ele também pede para calcularmos o momento máximo da viga. Para isso, vamos calcular primeiro o nosso momento de inércia:
E enfim a tensão de flexão é dada por:
Onde c é a distância até a fibra mais tracionada ou comprimida, e no nosso caso a maior tensão acontece quando c=h.
35 x 106 =