Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 44

Para a barra composta indicada, determine o raio de curvatura provocado pelo momento fletor 200   N m

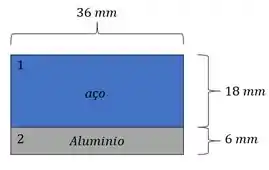
Passo 1

Quando temos mais de um material na nossa barra precisamos converter um deles para facilitar o nosso cálculo.

Sabemos que o nosso fator a ser calculado é dado por:

n = E p a r t e   t r a n s f o r m a d a   E p a r t e   i n t a c t a  

Vamos transformar então o alumínio em uma correspondente em aço.

n = E a l u m i n i o   E a ç o   = 70 210 = 0,33

E para mudarmos a largura do alumínio precisamos fazer a seguinte conta.

b ' = n b = 0,33   .   36 = 12   m m

Sendo assim a nova seção é dada por:

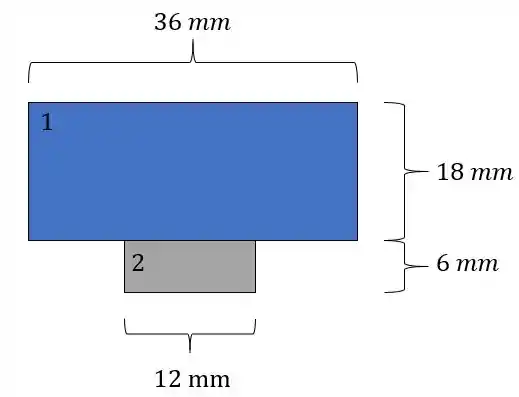
Nosso objetivo é determinar o raio de curvatura dado pela seguinte equação:

1 ρ = M I E

Mas para podermos determinar o momento de inércia, precisamos determinar a linha neutra, e a linha neutra vai ser dada pela seguinte equação:

y - = A 1 y 1 + A 2 y 2 A 1 + A 2

Sabendo que as dimensões são dadas por:

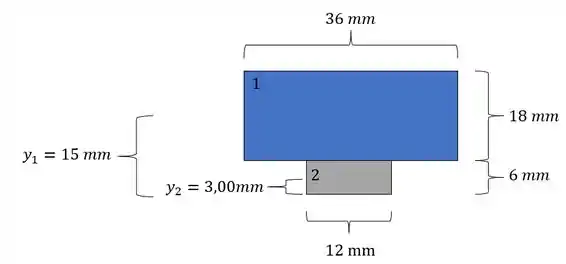
Assim temos que:

A 1 = 36 × 18 = 648   m m 2

A 2 = 12 × 6 = 72   m m 2

y - = 648 × 15 + 72 × 3,0 648 + 72 = 13,8   m m

Passo 2

Agora que temos a LN, podemos determinar o momento de inércia, o momento de inércia vai ser dado pela seguinte equação:

I = I 1 + I 2 + ( A 1 d 1 2 + A 2 d 2 2 )

Em que as áreas já definimos no passo anterior, e os valores de I 1   e   I 2 são os momentos de inércia de cada uma das seções mais simples, e d 1   e   d 2 são as distâncias do centroide de cada uma das peças mais simples até a LN. Assim as medidas da nossa seção são dadas abaixo.

Além disso temos que:

A 1 = 36 × 18 = 648   m m 2

A 2 = 12 × 6 = 72   m m 2

I 1 = b h 3 12 = 36 × 18 3 12 = 17496   m m 4

I 2 = b h 3 12 = 12 × 6 3 12 = 216   m m 4

Assim a inercia da nossa seção vai ser dada por:

I = I 1 + I 2 + ( A 1 d 1 2 + A 2 d 2 2 )

I = 17496 + 216 + ( 648 × 1,2 2 + 72 × 10,8 2 )

I = 27043,2   m m 4

E lembra que o nosso objetivo é determinar o raio de giração, e sabemos que o cálculo é feito da seguinte maneira:

1 ρ = M I E

ρ = E I M

Como tudo foi convertido para aço, podemos usar o modulo de elasticidade do aço, sendo assim teremos que:

E = 210   G P a = 210000   M P a = 210000   N / m m 2

I = 27043,2     m m 4

M = 200   N m = 200000   N m m

ρ = 210000   N m m 2 27043,2   m m 4 200000     N m m = 28395,4   m m = 28,4   m

Resposta

ρ = 28,4   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a cantoneira e o carregamento do Problema 6.81, determine a distribuição de tensões de cisalhamento ao longo da linha D ' A ' na aba vertical
Três pranchas são pregadas juntas de modo a formar a viga mostrada, a qual está submetida a uma força cortante vertical. Sabendo que o espaçamento entre os pregos é s = 75m m e a força cortante admiss
Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante
Uma viga de paredes finas de espessura uniforme tem a seção transversal mostrada na figura. Determine a dimensão b para a qual o centro de cisalhamento O da seção transversal está localizado no ponto
A viga balanço AB, consistindo de um tubo de paredes finas com raio médio de 31,8m m e espessura de parede de 6,35m m . está submetida passa a uma força vertical de 2224k N . Sabendo que a linha de aç